高三数学统练八立体几何（一）

高三数学统练八立体几何（一）

 一． 选择题：

　1．下列四个命题：①若a, b是两条异面直线，P为空间任意一点则过P点有且只有一个平面与a, b都平行； ②若α、β、γ是三个不同的平面，a表示直线，如果α∩β=a，α⊥γ，β⊥γ，则a⊥γ；③若AB、CD是异面直线，则AC、BD也一定是异面直线。其中正确命题的个数是（  ）。

　（A）1　 （B）2　 （C）3　 （D）0

　2．两条互相垂直的异面直线a和b，a⊥平面α，b⊥平面β，则α与β（　）。

　（A）一定垂直 （B）一定相交但不一定垂直 （C）相交或平行 （D）一定平行

　3．已知a, b为异面直线，点A、B在直线a上，点C、D在直线b上，且AC=AD，BC=BD，则直线a, b所成的角为（　）。

　（A）90°　 （B）60°　 （C）45°　 （D）30°

　4．已知m, l为直线，α, β为平面，给出下列五个命题：① 若l垂直于α内的两条相交直线，则l⊥α；② 若l//α，则l平行于α内所有直线；③ 若mα,lβ,且l⊥m，则α⊥β；④ 若lβ，且l⊥α，则α⊥β；⑤ 若mα,lβ,且α//β，则m//l，其中正确的命题是（　）。

　（A）①④　 （B）①②④　 （C）①③⑤　 （D）③④⑤

　5．设两平面α、β和直线l，下列三个条件：① l//α；② α//β；③ l//β，若以其中两个作为条件，另一个作为结论，则可构成三个命题，这三个命题中，正确命题的个数是（ D ）。

　（A）3　 （B）2　 （C）1　 （D）0

　6．P是△ABC所在平面外一点，则点P在此三角形所在平面上的射影是△ABC的垂心的充分必要条件是（　）。

　（A）PA=PB=PC　

（B）PA⊥BC，PB⊥AC 

　（C）点P到△ABC三边所在直线的距离相等

　（D）PA、PB、PC与平面ABC所成的角相等

　7．在一个四面体中，如果它有一个面是直角三角形，那么它的另外三个面（）

　 （A）至多只能有一个直角三角形　　(B)至多只能有两个直角三角形

(C)可能都是直角三角形　　　　　  (D)一定都不是直角三角形

　8．已知长方体ABCD－A₁B₁C₁D₁中，底面是边长为2的正方形，高为4，则点A₁到截面AB₁D₁的距离是（　）。

　（A）　 （B）　 （C）　 （D）

　

　二．填空题：

　9．AB是平面α的一条斜线段，B是斜足，AA’⊥α，A’是垂足，BCα，若∠ABC=60°，∠A’BC=45°，则AB与平面α所成的角是　　　　　　　　　　　　 .

　10．点A、B到平面α的距离分别是12、20，若斜线AB与平面α成30°角，则AB的长等于　　　　　　　　　　　　　　 。

　11．若E、F、G、H分别是三棱锥A－BCD的棱AB、BC、CD、DA的中点，则三棱锥A－BCD满足条件　　　　　　　　　　　　　  时，四边形EFGH是矩形。(填上你认为正确的一种条件即可，不必考虑所有可能的情况)

　12．已知m, l是直线，α、β、γ是平面，给出下列命题：

① β∩γ=l, l//α,mα, m⊥γ, 则α⊥γ且m//β；

② 若lβ且l⊥α，则α⊥β；

③ 若β∩γ=l, l//α, mα和m⊥γ，则α⊥γ且l⊥m；

④ 若mα, lβ, 且α//β，则m//l；

⑤ 若m//α, mβ, α∩β=l，则m⊥l，

其中所有正确命题的序号是　　　　　　　　　　　　　　　　  。

　13．在正方体ABCD－A₁B₁C₁D₁中，M为DD₁中点，O为底面ABCD的中心，P为棱A₁B₁上任意一点，则直线OP与直线AM所成的角是 　　　　　　　 。

　14．a, b为不垂直的异面直线，平面α、β分别过直线a、b，则① α∥β；② α⊥β；③直线a//β；④ 直线a⊥β 。四种情况可能出现的有　　　　 。

　　三、解答题

15．如图 在长方体ABCD－A₁B₁C₁D₁中，已知AB=BC=3，BB₁=4，连接B₁C，作BE⊥B₁C，交CC₁于E，交B₁C于F，（1）求证：A₁C⊥平面EBD；（2）求点C到平面EBD的距离。

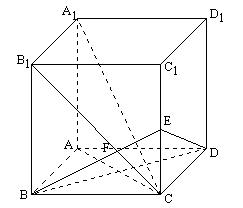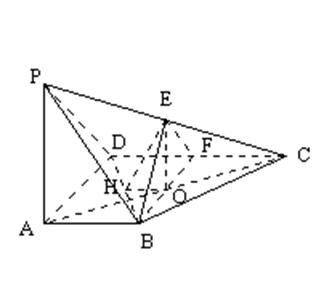
16．如图，四棱锥P－ABCD的底面为一直角梯形，BA⊥AD，CD⊥AD，CD=2AB，PA⊥底面ABCD，E为PC中点，（1）证明：平面PDC⊥平面PAD；

（2）证明：EB∥平面PAD；（3）若PA=AD，证明：BE⊥平面PDC。

答案：BAAA　DBCC　 9. 　　 10.16或64　　　 11.　　　　12.②③　 13. 　　  14.①②③　　　　15.（2）　　　　16.（略）