高三数学统练三函数（3）
班级 姓名 学号 成绩
一、 选择题：（每题5分，共50分）
1．函数y=lg(
)的图象关于（
）.
（A） x轴对称 （B）y轴对称 （C）原点对称 （D）直线y= x对称
2．若a, b∈R，那么
成立的一个充分非必要条件是（
）.
（A）a>b （B）ab(a－b)<0 （C）a<b<0 （D）a<b
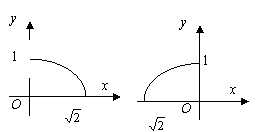
3．若函数y=f (x)是函数y=－
(0≤x≤1)的反函数，则y=f
(x)的图象（ ）.
 | |||||
 | |||||
 | |||||
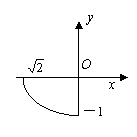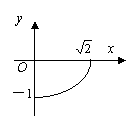（A） （B） （C） （D）
4．已知定义在R上的偶函数y=f(x)在[0, +∞]上为增函数，且f(
)=0，则满足f(log
x)>0的x的取值范围是（ ）.
（A）(0, 
) （B）(2, +∞) （C）(, 1)∪(2, +∞) （D）(0, )∪(2, +∞)
5．设a适合
>0, x>1，若f (x)=ax, g(x)=x
, p(x)=logax，则f (x)、g(x)、p(x)的大小关系是（ ）.
（A）f(x)<g(x)<p(x) （B）p(x)<f(x)<g(x)
（C）p(x)<g(x)<f(x) （D）f(x)<p(x)<g(x)
6．指数函数y=(a－1)x与y=
具有不同的单调性，则M=(a－1)
，N=
的大小关系是（
）.
（A）M<N （B）M=N
（C）M>N （D）不能确定
7．若a>b, f (x)在[b, a]上单调递减，则y=f －1(x)必满足（ ）.
（A）在[b,a]上也是单调递减 （B）在[f (b), f (a)]上是单调递减
（C）在[f －1(a), f －1(b)]上是单调递减 （D）在[f (a), f (b)]上是单调递减
8、对于x∈[0，1]的一切值，a+2b>0是使ax+b>0恒成立的（ ）.
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
9．函数f (x)=
的单调递增区间是（
）.
（A）[－6,-2]和[2, +∞] （B）(－2, +∞)
（C）(－∞, －6) 和(－2, 2) （D）[－6, 2]
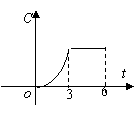
10．某工厂六年来生产某种产品的情况是：前三年年产量的增长速度越来越快，后三年年产量保持不变，则该厂六年来这种产品的总产量C与时间t（年）的函数关系可用图像表示的是（ ）.
 | |||||||
 |  |  | |||||
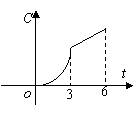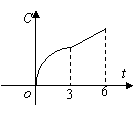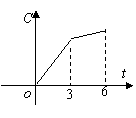（A） （B） （C） （D）
二、填空题（每小题4分，共16分）
11、方程
的解为
.
12．已知函数y=f (2x－1)的定义域为[－1, 1]，则函数y=f [lg(x－)+1]的定义域为 .
13．已知y=loga+1(2－ax) (a>－1,且a≠0)在[1, 2]上是x的减函数，则a的取值范围是 .
14．若函数y=a2x+2ax－1(a>0且a≠1)在区间[－1, 1]上的最大值为14，则a的值为 .
三、解答题：（第15，16题每题10分，第17题14分）
15．已知1≤x≤4，f (x)＝x2－2bx＋
(b≥1), f (x)的最小值为p，
(1) 试用b表示p；(2) 求p的最大值，并说明此时b的取值.
16．（满分10分）某农工贸集团开发的养殖业和养殖加工业的年利润分别为
和
（万元），与这两项生产与投入的资金
（万元）的关系是
，
。该集团今年计划对这两项生产投入总资金共60万元，为获得最大利润，对养殖业与养殖加工业生产每项各投入多少万元？可获得最大利润，最大利润是多少万元？
17．（满分14分）设函数
,方程
的两个实根为
,且
.
求证:(Ⅰ)为方程
的两个根;
（Ⅱ）若四次方程的另两个根为
,且
,试判断,的大小.
高三数学统练三 函数（3）答案
一．选择题：(每小题5分，共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 答案 | C | C | B | D | B | C | D | C | A | A |
|
二．填空题：(每小题4分，共16分)
| 11 | 1+log35 | 12 |
|
| 13 |
| 14 | 3或 |
三．解答题：（第15，16题每题10分，第17题14分）
15、解：(1) 1≤x≤4，f (x)＝x2－2bx＋＝(x－b)2－b2＋
, (b≥1), （1分）
∴ 当1≤b≤4且x＝b时,最小值 p＝－b2＋, （3分）
当b>4且x＝4时, p＝16－
b,
（5分）
(2) 当1≤b≤4时, p＝－(b－
)2＋
, ∴ b＝1时，pmax＝－
. （7分）
当b>4时, p<16－×4＝－15, ∴ b＝1时,pmax＝－.
（10分）
16、解:设对养殖加工业投入x万元，则对养殖业投入60－x万元, （2分）
年利润=P+Q=
+
=－x+
+20,
（4分）
当
=5即x=25时，年利润取得最大值
万元
（8分）
所以对养殖业投入35万元，养殖加工业投入25万元时
获最大利润万元
(10分)
17、解：（1）由函数满足
，得
，问题得证.
（5分）
（2）由
是方程的根，设
，则得
,于是，
，
记
，则
，
所以
的二个根
满足：
. （14分）