高三数学统练十二圆锥曲线
注意：1.统练时间 90分钟；2.选择题和填空题的答案填在第3页的答题表中.
一、选择题（每小题5分，共40分）
1. 椭圆短轴长是2，长轴是短轴的2倍，则椭圆中心到准线距离是（ ）
（A）
（B）
（C）
（D）
2.
（文科）中心在原点，准线方程为x=±4，离心率为
的椭圆方程是（ ）
（A）
（B）
（C）
（D）
（理科）已知点P的极坐标为
，那么过点P且垂直于极轴的直线的极坐标方程为( )
（A）
（B）
（C）
（D）
3.
抛物线
和
的焦点之间的距离为（ ）
(A) 
（B）
（C）
（D）
4. 设F1和F2 为双曲线
的两个焦点，点P在双曲线上， 且满足∠
=90°，则△的面积是（ ）
（A）
（B）
（C）1 （D）2
5．（文科）若 
表示焦点在y轴上的双曲线，则它的半焦距c的取值范围是（ ）
（A）（1，+∞） （B）（0，1） （C）（1，2） （D）与k有关，不确定
（理科）已知曲线C: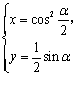
，若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为（ ）
（A）
（B） （C）
（D）
6. 把椭圆
绕它的左焦点按顺时针方向旋转90°，所得椭圆的准线方程是（ ）
（A）
（B）
（C）
（D）
7. 过双曲线
的右焦点F作直线交双曲线右支于A、B两点，线段AB的长为5
，将双曲线绕其右准线旋转120°，则由线段AB形成的曲面的面积为（ ）（注：
）
(A)40π （B）30π （C）20π （D）10π
8. 已知两点M（0，1），N（10，1），给出下列直线方程:
①5x-3y-22=0 ②5x-3y-52=0 ③x-y-4=0 ④4x-y-15=0
在直线上存在点P满足MP=NP+6的所有直线方程是（ ）
（A）①② （B）②③（C）③④ （D）④①
二、填空题（每小题5分，共30分）
9.抛物线
的焦点坐标为_______；准线方程为___________.
10. （文科）若椭圆
与双曲线
有相同焦点，则k=_____.
（理科）在极坐标系中，点
到直线
的距离是_____.
11. 已知抛物线的顶点在原点，焦点在x轴上，又抛物线上一点A（4，m）到准线的距离为6，则抛物线的方程为__________，m= _________.
12. （文科）与半圆
外切，且和x轴相切的动圆的圆心轨
迹方程为_________ .
（理科）在极坐标系中，曲线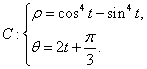
（t为参数）,化为直角坐标方程为_________.
13.设双曲线
的一条准线与两条渐近线相交于A、B两点，相应的焦点为F,以AB为直径的圆恰经过点F，则该双曲线的离心率为_________.
14. 已知直线l交椭圆
于M、N两点，B(0,4)是椭圆的一个顶点,若
ΔBMN的重心恰好位于椭圆的右焦点上，则直线l的方程为____________.
高三数学统练十二 圆锥曲线
2004.2.16
班级___________ 姓名_____________ 学号____________ 成绩___________
一、选择题（每小题5分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | A ；D | B | C | A；B | A | C | B |
二、填空题（每小题5分，共30分）
9．
； 10. 文 1 ， 理
；
11．
； 12. 
；
13．；
14.
.
三、解答题（每小题10分，共30分）
15.设椭圆C的一个焦点为
，相应的准线方程为
，离心率
（1）求椭圆C的方程；
（2）
为椭圆C的另一个焦点，P为椭圆C与函数
的图像的一个交点，试求
的值.
答案：（1）
（2）
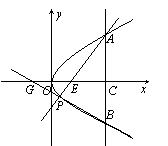
16.（理科学生作）已知抛物线
，直线AB垂直于x轴并与抛物线交于A、B两点，其垂足为C(如图甲).又E为线段OC上的一点，G为x负半轴上一点，且OE=OG，其中O为坐标原点.
求证：直线AE与BG的交点P在抛物线上.
（文科学生作）已知抛物线，直线l与抛物线交于A、B两点，O为坐标原点.若OA⊥OB,
且O在AB上的射影为D(2,1) (如图乙).
求此抛物线的方程.
答案:
17. （理科学生作）过点M(-2,0)作直线l交双曲线
于A、B两点，以OA、OB为
邻边作平行四边形OAPB.
(1)求P点的轨迹方程，并说明轨迹是什么曲线？
(2)是否存在这样的直线l，使四边形OAPB为矩形？若存在，求出直线l的方程；若不存在，请说明理由.
（文科学生作）中心在原点，焦点在x轴上的双曲线的方程为
，
直线
与双曲线相交，且截得线段的长为4，求双曲线的方程.
答案：（1）
,表示中心在（-2，0）的双曲线
且除去原点.（2）不存在；（文）
四、附加题（满分10分）
18.对于二次曲线系
和平面内任意一点
求证：总有
中一个椭圆和一条双曲线经过点M.
提示：构造函数
，
因为，
所以，方程
的两个实根
应满足