高中三年级教学质量检测数学试题(理科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,第I卷1至2页,第II卷3至8页,共150分,考试时间120分钟。
第I卷(选择题 共60分)
一. 本卷共12小题,每小题5分,共计60分。在每小题列出的四个选项中,只有一项是符合题目要求的。
1. 函数![]() 满足
满足![]() ,则f(0)的值为( )
,则f(0)的值为( )
A. 5 B. 6 C. -5 D. -6
2. 若a、b为实数,则使![]() 成立的一个充要条件为( )
成立的一个充要条件为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 设a,b,c分别是![]() 中∠A,∠B,∠C所对边的边长,则直线
中∠A,∠B,∠C所对边的边长,则直线
![]() 与
与![]() 的位置关系是( )
的位置关系是( )
A. 平行 B. 重合 C. 垂直 D. 相交但不垂直
4. 在约束条件![]() 下,
下,![]() 的最大值是( )
的最大值是( )
A. 9 B. 10 C. 11 D. 12
5. ![]() 为不共线的向量,且
为不共线的向量,且![]() ,以下四个向量中模最小者为( )
,以下四个向量中模最小者为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
6. 已知⊙A:![]() 及直线l:
及直线l:![]() ,⊙A上到l的距离为3的点共有( )
,⊙A上到l的距离为3的点共有( )
A. 1个 B. 2个 C. 3个 D. 4个
7. 双曲线![]() 中,直线l过
中,直线l过![]() ,原点到l的距离为
,原点到l的距离为![]() (c为双曲线的半焦距),则双曲线的离心率为( )
(c为双曲线的半焦距),则双曲线的离心率为( )
A. 2 B.
![]() C.
C.
![]() D.
D.
![]()
8. 设a,b是两条异面直线,给出下列四个命题:(1)存在分别经过直线a和b的两个互相平行的平面;(2)存在分别经过直线a和b的两个互相垂直的平面;(3)存在经过直线a与b垂直的平面;(4)存在与a,b都平行且距离相等的平面。其中正确命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
9. 已知![]() 是双曲线
是双曲线![]() 的左右焦点,P、Q为右支上的两点,直线PQ过
的左右焦点,P、Q为右支上的两点,直线PQ过![]() 且倾斜角为
且倾斜角为![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
8 C.
B.
8 C.
![]() D.
随
D.
随![]() 大小变化
大小变化
10. 正三棱锥![]() 中,E为SA的中点,F为
中,E为SA的中点,F为![]() 的中心,SA=BC,则异面直线EF与AB所成的角是( )
的中心,SA=BC,则异面直线EF与AB所成的角是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11. 方程![]() 的四个实数根组成一个首项为
的四个实数根组成一个首项为![]() 的等比数列,则
的等比数列,则![]() ( )
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
12. 一批救灾物资随26辆汽车从某市以v km/h的速度直达灾区,已知两地公路线长400km,为了安全起见,两辆汽车的间距不得小于![]() (汽车本身长度不计),那么这批物资全部运到灾区,至少需要( )
(汽车本身长度不计),那么这批物资全部运到灾区,至少需要( )
A. 5h B. 10h C. 15h D. 20h
第II卷(非选择题,共90分)
二. 填空题(每题4分,共16分)
13. ![]() ,则
,则![]() _____________。
_____________。
14. 过直线![]() 上一点M向圆
上一点M向圆![]() 作切线,则M到切点的最小距离为______________。
作切线,则M到切点的最小距离为______________。
15. 定点![]() 与抛物线
与抛物线![]() 上一点P之间的距离为
上一点P之间的距离为![]() 到准线的距离为
到准线的距离为![]() ,当
,当![]() 取得最小值时,点P的坐标为___________。
取得最小值时,点P的坐标为___________。
16. 设向量![]() ,规定两向量
,规定两向量![]() 之间的一个运算为
之间的一个运算为![]() ,若已知
,若已知![]() ,则
,则![]() _______。
_______。
三. 解答题(本大题共6个小题,满分74分。解答应写出文字说明、证明过程或演算步骤。)
17. (12分)
已知:在![]() 中,A、B、C的对边为a、b、c,且
中,A、B、C的对边为a、b、c,且![]()
(1)求![]() 的面积S的最大值。
的面积S的最大值。
(2)求a的最小值。
18. (12分)
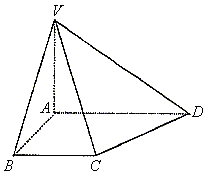
直角梯形ABCD中,BC∥AD,AD∥⊥AB,![]() ,VA⊥平面ABCD。
,VA⊥平面ABCD。
(1)求证:VC⊥CD。
(2)若![]() ,求CV与平面VAD所成的角。
,求CV与平面VAD所成的角。
19. (12分)
已知函数![]() 的图象经过原点。
的图象经过原点。
(1)若![]() 成等差数列,求m的值;
成等差数列,求m的值;
(2)若![]() ,正数a、b、c成等比数列,求证:
,正数a、b、c成等比数列,求证:![]()
20. (12分)
已知抛物线![]() 的一条焦点弦被焦点分成长为m、n的两部分。
的一条焦点弦被焦点分成长为m、n的两部分。
求证:![]() 为定值。
为定值。
21. (12分)
某厂家拟在2003年国庆节期间举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用m万元(![]() )满足
)满足![]() (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)
(1)将2003年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2003年的促销费用投入多少万元时,厂家的年利润最大?
22. (14分)
已知椭圆![]() 的一条准线方程是
的一条准线方程是![]() ,其左、右顶点分别是A、B;双曲线
,其左、右顶点分别是A、B;双曲线![]() 的一条渐近线方程为
的一条渐近线方程为![]() 。
。
(I)求椭圆![]() 的方程及双曲线
的方程及双曲线![]() 的离心率;
的离心率;
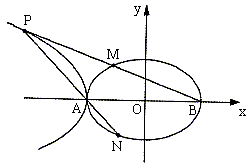
(II)在第二象限内取双曲线![]() 上一点P,连结BP交椭圆
上一点P,连结BP交椭圆![]() 于点M,连结PA并延长交椭圆
于点M,连结PA并延长交椭圆![]() 于点N,若
于点N,若![]() 。求证:
。求证:![]() 。
。
【试题答案】
一. 选择题(60分)
1. B 2. D 3. C 4. C 5. A 6. C
7. C 8. C 9. A 10. A 11. B 12. B
二. 填空题。
13. 7 14.
![]() 15.
(2,2) 16.
(-2,1)
15.
(2,2) 16.
(-2,1)
三. 解答题。
17. (12分)
解:(1)![]()
![]() ………(5分)
………(5分)
![]() ………………(6分)
………………(6分)
(2)![]() ………………(分)
………………(分)
![]() ………………(10分)
………………(10分)
![]() …………………(11分)
…………………(11分)
![]() ………………………(12分)
………………………(12分)
18. (1)连结AC
![]()
取AD中点G,连CG,则ABCG为正方形
又![]()
![]()
![]() …………………………(4分)
…………………………(4分)
VA⊥平面ABCD,DC⊥AC
由三垂线定理:VC⊥CD………………(6分)
(2)连VG,由![]() 面VAD
面VAD
![]() 是CV与平面VAD所成的角………………(9分)
是CV与平面VAD所成的角………………(9分)
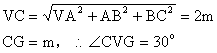
∴CV与平面VAD所成角为![]() ………………………(12分)
………………………(12分)
19. 解:(1)将(0,0)代入![]() ,得:
,得:![]()
![]() ………………(2分)
………………(2分)
由已知可得:![]() ………………(3分)
………………(3分)
即:![]()
![]() (
(![]() 舍)……………………(6分)
舍)……………………(6分)
(2)由已知可得:
![]()
![]()
![]() ………………………(8分)
………………………(8分)
而![]()
![]()
![]() ………………………(12分)
………………………(12分)
另解:![]() …………………(8分)
…………………(8分)
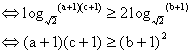
![]() ………………(10分)
………………(10分)
∵a,b,c成等比数列
![]()
![]() 得证………………(12分)
得证………………(12分)
20. 解:由题可知,焦点坐标为(1,0)
当焦点弦AB与对称轴垂直时,![]()
![]() ………………………(4分)
………………………(4分)
当焦点弦AB与对称轴不垂直时,设其方程为![]()
将其代入抛物线![]()
有![]() …………………………(6分)
…………………………(6分)
令![]()
则![]()
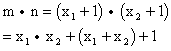
![]() ………………(10分)
………………(10分)
![]() ,即
,即![]()
综上可知![]() 为定值。………………(12分)
为定值。………………(12分)
21. 解:(1)设2003年生产产品x万件
![]() 时,
时,![]() 代入
代入
![]() ………………(2分)
………………(2分)
则年成本:![]() ………………(4分)
………………(4分)
年利润:![]() …………(6分)
…………(6分)
![]() ……………………(7分)
……………………(7分)
(2)![]() ………………(10分)
………………(10分)
当且仅当![]() ,即
,即![]() 时取等号………………(11分)
时取等号………………(11分)
![]() 时,
时,![]() 万元……………………(12分)
万元……………………(12分)
22. 解:(I)由已知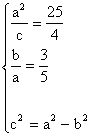 ,解之得:
,解之得:![]() …………(3分)
…………(3分)
∴椭圆的方程为![]() ,双曲线的方程
,双曲线的方程![]()
又![]()
∴双曲线的离心率![]() ………………(7分)
………………(7分)
(II)由(I)![]()
设![]() 则由
则由![]() 得M为BP的中点
得M为BP的中点
∴P点坐标为![]()
将M、P坐标代入![]() 方程得:
方程得:
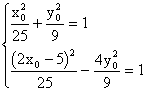
消去![]() 得:
得:![]()
解之得:![]() 或
或![]() (舍)
(舍)
由此可得:![]() ………………(9分)
………………(9分)
当P为![]() 时,
时,![]()
即:![]()
代入![]() ,得:
,得:![]()
![]() 或
或![]() (舍)
(舍)
![]()
MN⊥x轴,即![]() ………………(14分)
………………(14分)
| 年级 | 高三 | 学科 | 数学 | 版本 | 期数 | ||||||||
| 内容标题 | 德州市高中三年级教学质量检测——数学试题(理科) | ||||||||||||
| 分类索引号 | G.624.6 | 分类索引描述 | 考试试题与题解 | ||||||||||
| 主题词 | 德州市高中三年级教学质量检测——数学试题(理科) | 栏目名称 | 名校题库 | ||||||||||
| 供稿老师 | 审稿老师 | ||||||||||||
| 录入 | 李红英 | 一校 | 康纪云 | 二校 | 审核 | ||||||||