第二次高三测试数学试题
一、 选择题:（本大题共有12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.）
1.集合
的子集的个数是
（ ）
A. 无穷多 B. 32 C. 16 D. 8
2. 下列以x为自变量的函数中，属于指数函数的是 （ ）
A. 
(a>-1,且a≠0) B. 
C. 
D. 
3. 在数列
中,
,则
( )
A. 2001 B. 2002 C. 2003 D. 2004
4. 设
都是单位向量,则下列各式中成立的是
( )
A. 
B. 
C. 
5.
（ ）
A. 
B. 
C. 
D. 
6.
（ ）
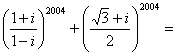A. 0 B. 2 C. 
D. 
7. 曲线
在点
处的切线方程是
( )
A. 
B. 
C. 
D. 
8. （本小题分为甲,乙两题,选作其中一题.若两题都作,则按甲题给分）
甲:已知
在
上是增函数,则
的取值范围是 ( )
A. 
B. 
C. 
D. 
<<3
乙：抛掷两颗骰子，所得点数之和记为
，则
表示的随机试验的结果是 （ ）
A. 两个都是4点 B. 一个是1点,另一个是3点
C. 两个都是2点 D. 一个是1点.另一个是3点;或两个都是2点
9. 一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角之间的关系是 （ ）
A. 相等 B. 互补 C. 相等或互补 D.不能确定
10. 三棱锥的三条侧棱两两垂直,其长分别为
,则三棱锥的外接球的球面面积为
（ ）
A. 
B.
C. 
D. 
11. 若命题
的逆命题是
,命题的否命题是
,则是的 （ ）
A. 逆命题` B. 逆否命题 C. 否命题 D. 以上结果都不对
12. 二次函数
在X轴上截得的线段的长度依次为
则
（ ）
A.1 B. 2 C. 3 D. 4
二﹑填空题 (本大题共四小题,每小题4分,共16分.请把答案写在题中的横线上.)
13.函数
的单调增区间是
.
14. 若不等式
的解集为
,则不等式
的解集为
.
15. 已知
的反函数是
则
的值是 .
16. 设
表示平面,
表示直线且
,给出四个论断: ①
∥
;②∥
;③
;④
,若以其中三个论断作条件,余下一个作结论,可构造出四个命题,写出你认为正确的一个命题
.(注:写法如“( )﹑( )﹑( )
( )”,只需在( )填上论断的序号即可.)
三﹑解答题(本大题共6小题,共74分,解答要写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
解不等式 
18.(本小题满分10分)
△ABC中,最大角∠C是最小角∠A的两倍.三边
是三个连续的正整数.求的值.
19.(本小题满分15分)
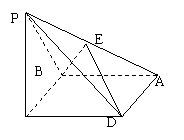如图,四棱锥P-ABCD中,底面是边长为的菱形,
,
平面
;
为
的中点.
(1) 求证:平面
平面;
(2) 求点
到平面
的距离;
(3)
|
的大小.
20.(本小题满分12分)
某厂为适应市场需求,投入98万元引进世界先进设备,并马上投入生产，第一年需各种费用12万元，从第二年开始，每年所需费用会比上一年增加4万元.而每年因引入该设备可获得年利润为50万元.请你根据以上数据,解决以下问题:
(1)引进该设备多少年后,开始盈利?
(2)引进该设备若干年后.有两面种处理方案:
第一种:年平均利润达到最大值时，以26万元的价格卖出.
第二种:盈利总额达到最大值时,以8万元的价格卖出. 问哪种方案较为合算?
21.(本小题满分12分)
已知函数
是偶函数,
是奇函数,正数数列满足
(1)求的通项公式.
(2)求
的前
项和.
22.(本小题满分15分)
设函数
(1)求证:无论为何实数,
总是增函数.
(2)确定的值,使为奇函数.
(3)当为奇函数时,求的值域.
第二次高三数学测试数学试题参考答案
一、 选择题：DABC CBC（CD） DABA
二﹑填空题：13.
；14.
或
；14.
；16.①②④③或①③④②
三、17.解：
由
或
4分
0或
，
或
8分
所以，原不等式的解集为
或
10分
18.解:
依题意有
，所以可设
2分
由正弦定理
6分
又， 
8分
由
9分 所以，的值依次为4，5， 6 . 10分
19.解:
(1)
证明:设AC,BD相交于O,连EO,易知
∥
，又,平面ABCD，所以EO⊥平面ABCD.而EO
平面EBD，所以平面EBD⊥平面ABCD,
5分
（2）
∥PC，∴EO∥平面PCD，∴E到平面PCD的距离等于O到平面PCD的距离.作OF⊥CD，F为垂足.可得OF⊥平面PCD.∴OF为O到平面PCD的距离.又,易知△BCD为正△,OF为DC边上的高的一半.∴
.即距离为
10分
(3)作OG⊥BE,垂足为G,连AG,∵平面EBD⊥平面ABD,AO⊥BD,∴AO⊥平面EBO.由三垂线定理知AG⊥BE.∴∠AGO为所求二面角的平面角,在Rt△EOB中，EO=OB=
，OG=
.AO=
,
∴tan∠AGO=
.所求二面角的大小为arctan
.
15分
20.解:
(1)设引进该设备x年后开始盈利.盈利额为y万元.
则
,
令y>0,得
.即引进该设备三年后开始盈利
6分
(2)第一种:年平均盈利为
,
, 当且仅当
,即
时,年平均利润最大,共盈利
万元.
第二种:盈利总额
，当
时,取得最大值102,即经过10年盈利总额最大,共计盈利
万元两种方案获利相等,但由于方案二时间长,所以采用方案一合算.
12分
21.解：
(1)由是偶函数得b=0,
是奇函数得C=0,
2 分.
由
或
是正数数列, 
是以1为首项的等比
数列,公比为
8分
(2).数列的通项为
,其前n项和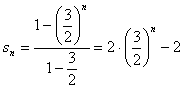
12分
22.解：
(1)
证:函数定义域为R,设
,则
.即
.所以,无论为何实数,总是增函数
5分.
(2).因为定义域为R, 所以要使为奇函数,必须
., 由
=1.所以,当
时,是奇函数.
10分
(3)当是奇函数时,有
,令
,
.所以的值域是
.
15分.