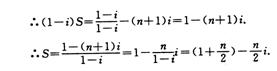4．1 复数的概念
一．选择题：
1．设集合I=C={复数}，R={实数}，M={纯虚数}，那么（ ）
（A）R∪M=C （B）R∩M={0} （C）R∪
=C （D）C∩=M
2．设z1, z2为复数，那么z12+z22=0是z1和z2同时为零的（ ）
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）非充分非必要条件
3．若(m2－m)+(m2－3m+2)i是纯虚数，则实数m的值为（ ）
（A）1 （B）1或2 （C）0 （D）－1, 1, 2
4．若实数x, y满足(1+i)x+(1－i)y=2，则xy的值是（ ）
（A）1 （B）2 （C）－2 （D）－3
5．下列命题中，假命题的个数是（ ）
① 虚轴上的点都表示纯虚数；② 复平面内纵坐标轴上的单位长度是i；③两个复数不能比较大小；④ 复数a1+b1i与a2+b2i (a1, a2, b1, b2∈R)相等的充要条件是a1=a2或b1=b2.
（A）1个 （B）2个 （C）3个 （D）4个
6．下列命题中，正确命题的个数是（ ）
①
是纯虚数；② z1+z2∈R
；③ (3+i)－(1+i)=23+i>1+i.
（A）0个 （B）1个 （C）2个 （D）3个
二．填空题：
7．复平面内，复数2－3i对应的点关于x轴、y轴和原点对称的点所表示的复数分别是 。
8．已知复数z=(a2－5a+6)+(a2－2a－1)i的对应点位于y轴的正半轴上，那么实数a= 。
9．已知i3m=in (m, n∈Z)，则im+n= 。
10．如果虚数z满足z3=8，那么z2+z2+2z+2的值是 。
11．复数z=sinθ(2sinθ－1)+(3sin2θ－1)i是纯虚数，则θ= 。
三．解答题：
12．已知平行四边形的三个顶点分别对应复数2i，4－4i，2+6i，求第四个顶点对应的复数。
13．已知方程x2－(tanθ+i)x－(i+2)=0,
（1）若方程有实根，求θ及其两根；
（2）证明无论θ为何值，此方程不可能有纯虚数根。
14．设n是4的倍数，试求和S=1+2i+3i2+4i3+……+(n+1)in.
