高等学校招生全国统一考试数学
一. 选择题（共12小题，每题5分，计60分）
1．已知平面向量
=（3，1），
=（x，–3），且
，则x=
（ ）
A. –3 B. –1 C. 1 D . 3
2.已知
则
( )
A.
B.
C. 
D.
3.设函数
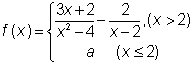在x=2处连续,则a=
( )
A.
B.
C.
D.
4.
的值为
( )
A. –1
B.0
C. 
D.1
5.函数f(x)
是
( )
A.周期为
的偶函数 B.周期为的奇函数 C. 周期为2的偶函数
D..周期为2的奇函数
6.一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 ( )
A.0.1536 B. 0.1808 C. 0.5632 D. 0.9728
7.在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 ( )
A. 
B.
C.
D. 
8. 若双曲线
的焦点到它相对应的准线的距离是2，则k= （ ）
A. 6 B. 8 C. 1 D. 4
9.当
时,函数
的最小值是
( )
A. 4 B. C.2
D.
10. 变量x、y满足下列条件：
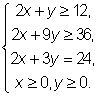则使z=3x+2y的值最小的（x，y）是
A. ( 4.5 ,3 ) B. ( 3,6 ) C. ( 9, 2 ) D. ( 6, 4 )
11. 若
则
A. 
B. 
C. 
D. 
12. 如右下图,定圆半径为 ( b ,c ), 则直线ax+by+c=0
与直线 x–y+1=0的交点在( )
A. 第四象限
B. 第三象限
C.第二象限
D. 第一象限
二.填空题(共4小题，每题4分，计16分）
13. 某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 (用分数作答)
14. 已知复数z与 (z +2)2-8i 均是纯虚数,则 z = .
51. 由图(1)有面积关系: 
则由(2) 有体积关系:
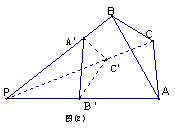
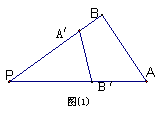
16. 函数
的反函数
三.解答题(共6小题,74分)
17. (12分)已知
成公比为2的等比数列(
也成等比数列. 求
的值.
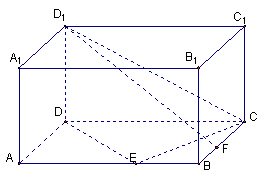18. 如右下图,在长方体ABCD—A1B1C1D1中,已知AB= 4, AD =3, AA1= 2. E、F分别是线段AB、BC上的点，且EB= FB=1.
(1) 求二面角C—DE—C1的正切值;
(2) 求直线EC1与FD1所成的余弦值.
19. (12分)设函数
(1) 证明: 当0< a < b ,且
时,ab >1;
(2) 点P (x0,
y0 ) (0< x0 <1 )在曲线
上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
20 (12分)某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)
21. (12分)设函数
其中常数m为整数.
(1) 当m为何值时,
(2) 定理: 若函数g(x) 在[a, b ]上连续,且g(a) 与g(b)异号,则至少存在一点x0∈(a,b),使g(x0)=0.
试用上述定理证明:当整数m>1时,方程f(x)= 0,在[e-ｍ-m ,e2ｍ-m ]内有两个实根.
22．(14分)设直线
与椭圆
相交于A、B两点，又与双曲线x2–y2=1相交于C、D两点， C、D三等分线段AB. 求直线的方程.