高三数学选择与填空题训练（13）

高三数学

选择与填空题训练（13）

一．选择题

1．定义在R上的函数的导数，其中常数k>0，则函数在（　　）

　　　 A．（－∞，+∞）上递增　　　　　　　　　　　　　B．上递增

　　　 C．上递增　　　　　　　　　　　　　　　　D．（－∞，+∞）上递减

2．(理做) 已知函数是区间[－1，+∞]上的连续函数，当，则f(0)=（　　）A．　B．1　 C．　D．0

（文做）直线与坐标轴所围成的三角形的面积为　　　 （　　）

　　　 A．　　　　　　　　　　　B．2　　　　　　　　　　　　C．1　　　　　　　　　　　　D．

3．已知函数和，其中，则它们反函数的图象关于（　　）

　　　 A．x轴对称　　　　　　 B．y轴对称　　　　　　 C．直线对称　D．原点对称

4．函数是R上的偶函数，且在上是增函数，若，则实数a的取值范围是　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　B．　　　　　　　C．　　　 D．

5．等差数列，若在每相邻两项间各插入一个数，使之成等差数列，那么新的等差数列的公差是（　　） A． B．－ C． D．－1

6．设是三个不重合的平面，l是直线，给出下列命题　　　　　　　　　　　　　　　　　

　　　 ①若，则；　　　　　　②若l上两点到的距离相等，则；

③若④若其中正确的命题是(　 )

　　　 A．①②　　　　　　　　　 B．②③　　　　　　　　　 C．②④　　　　　　　　　 D．③④

7．对某种产品的5件不同正品和4件不同次品一一进行检测，直到区分出所有次品为止. 若所有次品恰好经过五次检测被全部发现，则这样的检测方法有（　　）

　　　 A．20种　　　　　　　　　B．96种　　　　　　　　　C．480种　　　　　　　　D．600种

8．棱长都为2的直平行六面体ABCD—A₁B₁C₁D₁中，∠BAD=60°，则对角线A₁C与侧面DCC₁D₁所成角的正弦值为（　　）A．B．C．D．

9．椭圆的左准线为l，左、右焦点分别为F₁，F₂，抛物线C₂­的准线为l，焦点是F₂，C₁与C₂的一个交点为P，则PF₂的值等于　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．4　　　　　　　　　　　　D．8

10．如图，南北方向的公路l，A地在公路的正东2km处，

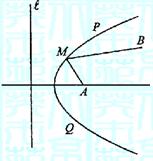
　　B地在A地东偏北30°方向2km处， 河流沿岸

PQ（曲线） 上任一点到公路l和到A地距离相等.现

要在曲线PQ上选一处M建一座码头，向A、B两地

转运货物，经测算从M到A， M到B修建公路的费

用均为a万元/km，那么修建这两条公路的总费用最低

是　　　　　　　　　　　　　　　　　　 （　　）

A．万元　B．万元C．5a万元D．6a万元

二．填空题

11．已知向量的值为　　　　 。

12．已知a>0，函数上是单调减函数，则a的最大值为　　　 。

13．过坐标原点且与点（）的距离都等于1的两条直线的夹角为　　　　　 .

14．等比数列中，

（理做）=　　　　　　 .（文做）　　　　　　 .

15．锥体体积V可以由底面积S与高h求得：. 已知正三棱锥P—ABC底面边长为2，体积为4，则底面三角形ABC的中心O到侧面PAB的距离为　　　　.

16．若函数满足：

　　　 对于任意成立，则称函数具有性质M.给出下列四个函数：①，②③，④.其中具有性质M的函数是　　　　　　 .

　　　 （注：把满足题意的所有函数的序号都填上）

B A（D）AD　BDCCB　C

11．1　 12．3　 13．30°　　 14． （）　　 15．　 16．①③