高考数学命题趋势预测试题

高考数学命题趋势预测试题

预测试卷（A）

一、选择题

1．设f：x→x²是集合A到集合B的映射，如果B=｛1，2｝，则A∩B只可能是（　　 ）

A．　　　　  B．或｛1｝　　　 C．｛1｝　　　　D．或｛2｝

2．定义在R上的函数f (x)的最小正周期为T，若函数y=f (x)，x∈(0,T)时，有反函数y=f^－1(x),x∈D。则函数y=f (x)，x∈(T,2T)的反函数为（　　 ）

A．y=f^－1(x),x∈D　　　　　  B．y=f^－1(x－T),x∈D

C．y=f^－1(x＋T),x∈D　　　　  D．y=f^－1(x)＋T,x∈D

3．已知函数y=f (x)满足2f (x)－f (，对于f (x)的图象，下列说法正确的是（　　 ）

A．图象上离x轴最近的点只有一点，这一点是（）

B．图象上离x轴最近的点只有两点，这两点是（）和（－）

C．图象上离x的最远的点只有一点，这一点是（－）

D．图象上离x轴最远的点只有两点，这两点是（）和（－）

4．已知定义在R上的函数y=f (x)满足以下三个条件：

①对于任意的x∈R，都有f (x+4)=f (x)；②对于任意的x₁、x₂∈R，且0 ≤x₁＜x₂≤2，都有f (x₁)＜f (x₂)；③函数y=f (x+2)的图象关于y轴对称。则下列结论中正确的是（　　 ）

A．f (4.5)＜f (7)＜f (6.5)　　　　　　　B．f (7)＜f (4.5)＜f (6.5)　

C．f (7)＜f (6.5)＜f (4.5)　　　　　　  D．f (4.5)＜f (6.5)＜f (7)　

5．已知α，β∈（），且tanα＜cotβ，则必有（　　 ）

A．α＜β　　　　B．β＜α　　　C．α＋β＜　　　　 D．α＋β＞

6．若(1+mx)⁶=a₀+a₁x+a₂x²+…+a₆x⁶，且a₁+a₂+a₃+…+a₆=63，则实数m的值是（　　 ）

A．3　　　　　　 B．1　　　　　 C．－3或1　　　　　　  D．3或－1

7．两个球的体积之和为12，它们的大圆周长之和为6，则它们的面积之和是（　　 ）

A．5　　　　　 B．10　　　　C．20　　　　　　　  D．24

8．若正三棱锥的侧面都是直角三角形，侧面与底面所成的角为（　　 ）

A．　　 B．　　 C．　　 D．

9．已知椭圆E的离心率为e，两焦点为F₁，F₂，抛物线C以F₁为顶点，F₂为焦点，P为两曲线的一个交点。若e，则e的值为（　　 ）

A．　　　　 B．　　　　　 C．　　　　 D．

10．已知圆C：x²+y²=1，点A(－2,0)及点B(2,a)，从A点观察B点，要使视线不被圆C挡住，则a的取值范围是（　　 ）

A．（－∞，－1）∪（1，＋∞）　　　　　　 B．（－∞，－2）∪（2，＋∞）

C．（－∞，－）∪（，＋∞）　　　 D．（－∞，－4）∪（4，＋∞）

11．已知点P（5cosθ，4sinθ），（0＜θ＜，若直线OP（O为原点）的倾斜角为α，则（　　 ）

A．α＜θ　　　　B．α＞θ　　　　C．α+=θ　　　　D．α+θ=

12．曲线S：y=3x－x³的过点A(2,－2)的切线（与x轴不平行），则在x轴上的截距是（　　 ）

A．16　　　　　  B．16或－2　　　 C．－　　　　D．

二、填空题

13．已知铜的单晶体的外形是简单几何体，单晶体有三角形和八边形两种晶面。如果铜的单晶体有24个顶点，每个顶点处有3条棱，那么单晶铜的三角形晶面和八边形晶面的数目分别为　　　　和

　　　　

14．已知△ABC中，，的夹角是

　　　　　 。

15．对某电子元件进行寿命追踪调查，情况如表：

寿命（h）	100～200	200～300	300～400	400～500	500～600
个数	20	30	80	40	30

估计电子元件寿命在200h～400h以内的频率为　　　　 

16．为了科学地比较考试的成绩，有些选拔性考试常常将考试分数转化为标准分，转化关系式为：

（其中x是某位学生的考试分数，是该次考试的平均分，s是该次考试的标准差，Z称为这位学生的标准分）。转化后的分数可能出现小数或负数，因此，又常常将Z分数作线性变换转化为其它分数。例如某次学业选拔性考试采用的是T分数，线性变换公式为：T=40Z+60。已知在这次考试中某位学生的考试分数是86，而他的T分数则为100，若这次考试的平均分为70，则这次考试的方差是　　　　  。

三、解题答

17．已知向量，定义f (x)=+m(m是实数)

（I）求f (x)的最小正周期

（II）求f (x)的单调递增区间

（III）若x ∈[0，]时，f (x)的最大值为4，求m的值

18．将4个编号的球随机地放入3个编号的盒中，对于每一个盒来说，所放的球数k满足0≤k≤4，假定各种放法都是等可能的，试求：

（I）“第一盒中恰有一个球”的概率；

（II）“第一盒中恰有2个球”的概率；

（III）“第一盒中恰有1个球而第二盒中恰有2个球”的概率。

19．如图，斜三棱柱为ABC－A₁B₁C₁，各棱长均为2，侧棱与底面所成角为，侧面ABB₁A_1­垂直于底面ABC，在平面ABB₁A₁内作B₁D⊥AB于D。

（I）求证：AB⊥平面B₁DC；

（II）求证：B₁C⊥C₁A；

（III）求四棱锥B－ACC₁A₁的体积。

20．设f (x)是定义在[－1，1]上的偶函数，g (x)的图像与f (x)的图像关于直线x=1对称，且当

x∈[2，3]时，g(x)=2a(x－2)－4(x－2)³，其中a为实常数。

（I）求f (x)的解析式；

（II）若f (x)在[0，1]上是增函数，求实数a的取值范围；

（III）是否存在正整数a，使函数f (x)的图像的最高点落在直线y=12上？若存在，试求出a的值，否则，请说明理由。

21．已知数列｛a_n｝的前n项的和为S_n，且满足（n≥2）

（I）数列｛｝是否为A·P？请证明你的结论。

（II）求S_n和a_n；（III）求证：²+S₂²+S₃²+…+S_n²≤

22．设抛物线过定点A（0，2），且以x轴为准线

（I）试求抛物线顶点M的轨迹C的方程；

（II）如果点P(a,1)不在线段y=1(－2≤x≤2)上，那么当a为何值时，存在曲线C上两点Q、R，使得

=0

【试卷A参考答案】

一、1. B　 2. D　 3. B　 4. A　 5. C　 6. C　 7. C　　8. B　 9. C　10. C　11. A　12. D

二、13.　8和6　　　 14.　150⁰　　　　15.　0.55　　　 16.　256　　

三、17. f ( x ) = 2sin ( 2x + ) + m + 1

（Ⅰ）T = π　　　（Ⅱ）[ kπ－, kπ＋]　()　　 （Ⅲ） 1

18. （Ⅰ）　　　　 （Ⅱ） 　　　　　　（Ⅲ）　　

19. （Ⅰ）CD⊥AB，B₁D⊥AB，　∴AB⊥面B₁DC。　　（Ⅱ）连BC₁交B₁C于O　BB₁C₁C是菱形，∴BC₁⊥B₁C　由（Ⅱ）知AC₁在面B₁C上的射影是BC₁　 ∴AC₁⊥BC₁ （Ⅲ）2

20．（Ⅰ）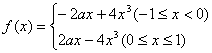

　 （Ⅱ）f′( x )≥0在[ 0，1 ]上恒成立，即2a－12x²≥0恒成立，a≥6x²在[ 0，1 ]上恒成立　　∴ a≥6

　 （Ⅲ）f′( x ) = 0　 ∴ x = 。若，即0 < a≤6 ，则[f ( x )]_max = f () = 2a－4 ()³ < 2a ·≤12　　　 ∴ 不合。　若 > 1 即 a > 6 时，f ( x ) 在[ 0，1 ]上增函数，∴[f ( x )]_max = f ( 1 ) = 2a－4 = 12　， ∴a = 8　。

21．（Ⅰ）n≥2时a_n = S_n－S_n－1　　 S_n－S_n－1 = －2 S_nS_n－1　　 ∴（n≥2）又　　∴｛｝是A·P。　　　　 （Ⅱ）S_n =

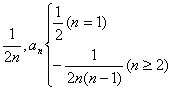
(Ⅲ)

≤

= 　 

22．（Ⅰ）由定义知：M（x，y）（y > 0）其焦点F（x，2y）。由抛物线定义知，即

，　 即。

　 （Ⅱ）设过P（a , 1）的直线为：y－1 = k（x－a），代入轨迹方程得：（1＋4k²）x²－8k²ax＋4（k²a²－1）= 0 。  △ = 16[ k²（4－a²）＋1 ]　 ∴

预测试卷（B）

一、选择题

1．已知映射f：A→B，其中A=B=R，对应法则f：y=x²+4x+7，x∈A，y∈B。对于集合B中的元素4，下列说法正确的是（　　 ）

A．在A中有1个原象　　B．在A中有2个原象　　C．在A中有3个原象　 D．在A中无原象

2．若函数y=f (x)存在反函数，则方程f (x)=c(c为常数)（　　 ）

A．有且只有一个实根　　B．至少有一个实根　　　 C．至多有一个实根　　 D．没有实根

3．下列四个命题：①若函数f (x)满足f (x－a)=f (a－x)，则函数f (x)的图象关于y轴对称；②若函数f (x)满足f (x－a)=f (a－x)，则函数f (x)的图象关于直线x=a对称；③函数y=f (x－a)与y=f (a－x)的图象关于y轴对称；④函数y=f (x－a)与y=f (a－x)的图象关于直线x=a对称。

其中正确的命题是（　　 ）

A．（1）与（2）　　 B．（3）与（4）　　　 C．（2）与（3）　　　　D．（1）与（4）

4．偶函数f (x)在[－1，0]上是减函数，则f (x)在[2，3]上是（　　 ）

A．增函数　　　　  B．先减后增的函数　　 C．减函数　　　　  D．先增后减的函数

5．设x∈，且cosx＜sinx＜，则x的取值范围是（　　 ）

A．　　　　 B．　　　 C．　　　　D．

6．已知(1－2x)⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵，则的值为（　　 ）

A．244　　　　　　  B．122　　　　　　 C．121　　　　　 D．242

7．表面积为4的球面上有三点A、B、C，而A和B，A和C之间的球面距离都是，B和C之间的球面距离是，则过A、B、C三点截面到球心的距离是（　　 ）

A．　　　　　  B．　　　　　  C．　　　　　 D．

8．在矩形ABCD中，AB=3，AD=4，PA⊥平面ABCD，PA=，那么二面角A－BD－P的度数是（　　 ）

A．30°　　　　　　  B．45°　　　　　　 C．60°　　　　　　 D．75°

9．如果以原点为圆心的圆，经过双曲线：=1的焦点，而且被该双曲线的右准线分为弧长为2：1的两段圆弧，那么该双曲线的离心率e等于（　　 ）

A．　　　　　  B．　　　　  C．　　　　D．

10．已知点P(a,b)(ab≠0)是⊙O：x²+y²=r²内一点，直线m是以P为中点的弦所在直线。若直线n的方程为ax+by=r²，则（　　 ）

A．m∥n，且n与⊙O相交　　　　　　 B．m∥n，且n与⊙O相离

C．m与n重合，且n与⊙O相离　　　　D．m⊥n，且n与⊙O相离

11．若P(2cosθ，sinθ)，θ∈[0，2且θ≠，B(0，)，以BP为边作正△BPQ，则△BPQ的面积的最大值为（　　 ）

A．　　　　　　　 B．2　　　　  C．3　　　　 D．4

12．曲线y=x²上点A处的切线与直线3x－y+1=0的夹角为45°，则点A的坐标为（　　 ）

A．（－1，1）　　　　 B．（）　　　 C．（1，1）　　 D．（－1，1）或（）

二、填空题

13．碳C₇₀分子有类似的球状多面体结构，它有70个顶点，以每个顶点为一端都有3条棱，各面是五边形或六边形，则C₇₀分子中五边形的个数为　　　　，六边形的个数为 　　　 。

14．已知平面上有A（－2，1），B（1，4），D（4，－3）三个点，又有一点C在上，使，连接DC，并延长至E，使，则E点的坐标为　　　　 。

15．将容量为100的样本数据，按从小到大的顺序号分为8个组，如下表

组号	1	2	3	4	5	6	7	8
频数	10	13	x	14	15	13	12	9

则第三组的频率为　　　　。

16．一个班级中的A、B两名学生的数学测验成绩如下：

A：60　　80　　70　　90　　70　　B：80　　65　　70　　80　　75

因为　　　　　　　 ，所以B的成绩较稳定。

三、解答题

17．已知向量。

求：（1）；（2）若f (x)=的最小值是－，求的值。

18．一个元件能正常工作的概率叫做这个元件的可靠性，由元件组成的系统能正常工作的概率称为系统的可靠性。设构成系统的每个元件的可靠性均为P(0＜P＜1，且各个元件能否正常工作是相互独立的。今有6个元件按下面图示的两种联接方式构成两个系统（I）和（II）。

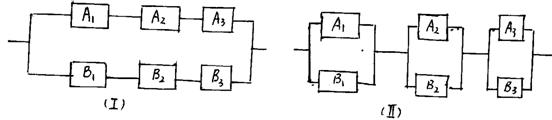
（1）试分别求出系统（I）和（II）的可靠性；

（2）试比较它们的可靠性的大小。

19．如图，已知直三棱柱ABC—A₁B₁C₁，AB=AC，F为棱BB₁上一点，BF：FB₁=2：1，BF=BC=2a。若D是BC中点，E是AD上异于A、D的任意一点。

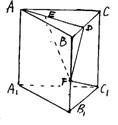（I）求证：DF是异面直线AD与C₁F的公垂线段，并求

其长度。

（II）若AB=2a，试问，在线段AD上的点E能否使EF与

平面BB₁C₁C成60°角，为什么？证明你的结论。

（III）若AB=2a，求F点到面ADC₁的距离。

20．已知f (x)=ax³+bx²+cx(a≠0)，在x=±1时取得极值，且f (1)=－1。

（1）试求常数a、b、c的值；

（2）试证明函数f (x)的极大值是f (－1)，极小值是f (1)；

（3）设F(x)=f (x)+m，不等式F(x)+2m²≥0在区间[－2，1]恒成立，求实数m的取值范围。

21．已知抛物线y²=2px(p＞0)，A、B是抛物线上不重合的任意两点，=0，，O为坐标原点。

（1）若，求点M的坐标。

（2）求动点M的轨迹方程，并指出其形状。

22．设数列｛a_n｝满足下列条件：

a₁=5,a_n+1=(n=1,2,3,…)，求证：

（1）a_n≥4(n=1,2,3,…)；

（2）a_n+1－4≤(a_n－4)　(n=1,2,3,…)。

【试卷B参考答案】

一、1. B　2. C　 3. D　 4. A　 5. B　 6. B　 7. C　 8. A　 9. D　 10. B　 11. C　 12. D

二、13.　12和15　　　 14. （）　　　 15.　0.14　　　  16.　S_A>S_B

三、17．（Ⅰ）　 （Ⅱ）f ( x ) = 2( cosx - λ)² ­­­­­­­- 2λ² – 1，

0≤cosx≤1 对λ分类讨论。0≤λ≤1，λ> 1和λ< 0。λ=

18．（Ⅰ）系统（Ⅰ）的概率P₁ = 1–（1–P³）² = P³（2–P³）。系统（Ⅱ）的概率P₂ = [ 1 -（1 - P）²]³ = P³（2–P）³　　 （0 < P < 1）

（2）P₁–P₂ = -6P³（ - 1）² < 0　　∴系统（Ⅱ）更可靠。

19．（Ⅰ）由勾股定理知DF⊥FC₁，又AD⊥BC，而面BB₁C₁⊥面A₁B₁C₁　　∴AD⊥DF。∴DF是AD与FC₁的公垂线段，DF =

（Ⅱ）假设存在时求出ED =  。E在DA的延长线上，而不在线段AD上，故不存在　　　 （Ⅲ）

20．（Ⅰ）f ′( x ) = 3ax² + 2bx + c , 又∵ = x ±1是极值点。∴f ′(±1 ) = 0　

∴

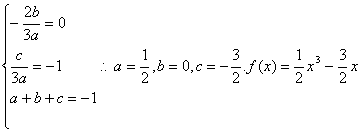
（Ⅱ）当x >1或x < －1时f ′( x ) > 0 。当－1< x < 1时f ′( x ) < 0

∴f ( x ) 在（－∞，－1）和（1，+∞）上是增函数，在（－1，1）上是减函数

x = －1时有极大值1，x = 1时有极小值－1

（Ⅲ）－2m²－m≤[ f ( x ) ]_min = －1　　　　 ∴m≥或m≤－1

21．（Ⅰ）A ( x₁ : y₁ )　 B ( x₂ : y₂)　 ∴y₁² = 2px₁　 y₂² = 2px₂　

∴x₁x₂ + y₁y₂ = 0　 又　　 ∴x₁² + y₁² = x₂² + y₂²　 ∴x₁ = x₂ , ∴y₂ =

　 ∴ x₁ = 2p　y₁ = 2p　　M ( 4p , 0 )　

（Ⅱ）　 ∴y₁y₂ = －4p² ,　 M ( x , y )　 ∴ y² = 2p ( x－4p )

22．（Ⅰ）a_n > 0　, a_n+1 =

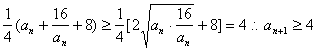
∵a₁ = 5 > 4　　 　∴a_n≥4　

（Ⅱ）∵（a_n+1－4）　∵a_n≥4

 n (1，2，3，4，……)。