高考数学模拟试卷
一、选择题（本大题共14小题，每小题4分，共56分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1、
的计算结果是（ ）
A、
B、
C、
D、
2、我国最长的河流长江全长约6300千米，用科学记数法表示为（ ）
A、
千米 B、
千米 C、
千米 D、
千米
3、正方形的对称轴一共有（）
A、l条 B、2条 C、3条 D、4条
4、如果
是锐角．且
，那么
的值是（ ）
A、
B、
C、
D、
5、把
分解因式的结果是（ ）
A、
B、
C、
D、
6、如果两个圆的半径分别为6cm和4cm，圆心距为10cm，那么这两个圆的位置关系为（ ）
A、内切 B、相交 C、外切 D、外离
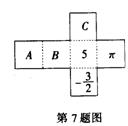
7、如图，是一个正方体纸盒展开图，按虚线折成正方体后，若使相对面上的两数互为相反数，则A、B、C表示的数依次是（ ）
A、
B、
C、
D
8、不等式组
的整数解的个数是（ ）
A、1个 B、2个 C、3个 D、4个
9、已知
，则（ ）
A、
B、
C、
D、
10、在
ABC中，点D、E分别在为AB、AC上，且DE//BC，若AD=2，DB=5，贝DE：BC：等于（ ）
A、
B、
C、
D、
11、反比列函数
的图象在第二、第四象限，则一次函数
的图象不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
12、直角梯形的中位线长a，一腰长b，这腰和底所夹的角是
，则它的面积为（ ）
A、
B、
C、
D、
13、已知AB是⊙O的直径，AC、AD是弦，且AB=2，
，AD＝l，则圆周角
CAD
的度数是（ ）
A、
或
B、
C、
D、
或
14、为了搞好2008年奥运会的硬件设施，北京市需对某些道路进行改造．甲、乙两工程队承担了亚运村到排球馆的道路扩建工程．甲、乙两队计划合作120天完成，但两队合作40天后，甲队因有其他紧急任务调离此工程，剩下的工程由乙队单独完成，所需时间恰好等于甲队单独完成整个工程所需要的时间，则甲队单独完成此项工程需（ ）
A、300天 B、200天 C、250天 D、225天
二、填空题（本大题共4小题，每小题4分，共16分．把答案填在题中横线上．）
15、函数
中，自变量
的取值范围是．
16、已知一组学生的身高如下：（单位：米）
1.70 1.62 1.71 1.59 1.60 1.64
这组数据的中位数是＿．
17、如图，已知AB是⊙O的直径，PC切⊙O于点C，
，则
等于____度.
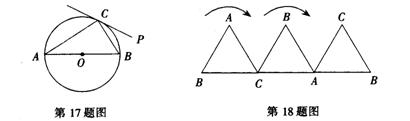
18、将形状为等边三角形的硬纸片沿水平线翻滚（如图所示），如果等边三角形的边长为1
那么点B从开始位置到结束所走过的路径长度为＿cm（用含
的式子表示）．
三、解答题（本大题共7小题，共48分．解答应写出文字说明、证明过程或演骤）
19、（本小题满分5分）
计算：
20、（本小题满分6分）
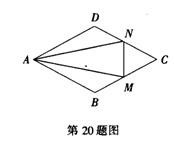
已知：如图，在菱形 ABCD中，点 M、N分别在 BC和 CD上，且
．
求证：
．
21、（本小题满分6分）
解方程：
22、金星中学某班前年暑假将勤工俭学挣得的班费2000元按一年定期存入银行，去年暑假到后取出1000元寄往灾区，将剩下的1000元和利息继续按一年定期存人银行，待今年毕业后全部捐给母校，若今年到期后取得人民币（本息和）1155元，问银行一年定期存款的年利率（假定年利率不变）是多少？
23、（本小题满分8分）
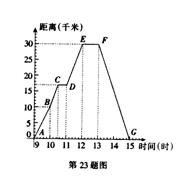
如图，图中的曲线表示小明星期日骑自行车外出离家的距离与时间的关系，小明九点离开家，十点回到家，根据这个曲线图，请你回答下列问题：
（1）到达离家最远的地方是几点？离家多远？
（2）何时开始第一次休息？休息时间多长？
（3）明在往返全程中，在什么时间范围内的平均速度最快？最快速度是多少？
（4）明何时距家21千米？（写出计算过程）
24、（本小题满分8分）
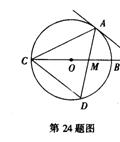
已知：如图，P是⊙O的直径CB延长线上的一点，PA切⊙O于点A．PA=15，PB=5，弦AD交CB于点M．
（1）若
，试判断CD与AP是否平行，并说明理由；
（2）求弦AC的长；
（3）当点D在⊙O上运动时，可以得到ACD的最大面积，请计算这个最大面积．
25、（本小题满分9分）
已知一次函数
的图象与反比例函数的图象交于M、N两点，且
．
（l）求反比例函数的解析式；
（2）若抛物线
经过M、N两点，证明：这条抛物线与轴一定有两个交点；
（3）设（2）中的抛物线与轴的两个交点为A、B（点A在点B左侧），与y轴交于点C，连结AC、BC.若
，求抛物线的解析式．
