高考数学普通高等学校招生全国统一考试仿真试卷

高考数学普通高等学校招生全国统一考试仿真试卷

数　学　理工农医类（六）

本试卷分第Ⅰ卷（选择题　共60分）和第Ⅱ卷（非选择题　共90分），考试时间为120分钟，满分为150分.

第Ⅰ卷（选择题　共60分）

参考公式：

如果事件A、B互斥，那么P（A+B）=P（A）+P（B）

如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）

如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的概率P_n（k）=p^k（1－p）^n－k

球的表面积公式S=4πR²，其中R表示球的半径

球的体积公式V=πR³，其中R表示球的半径

一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1.已知集合P={（x，y）x+y=1}，Q={（x，y）x²+y²≤1}，则

A.PQ　　　　　　　　　 B.P=Q　　　　　　　　　　　　 C.PQ　 　　　　　 　 D.P∩Q=Q

2.已知函数f（x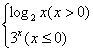）=，则f［f（）］的值是

A.9　　  　　　　　　　　　　B.　　  　　　　　　　　　C.－9　　　　　　　　　　　D.－

3.将直线x+y=1绕（1，0）点顺时针旋转90°后，再向上平移1个单位与圆x²+(y－1)²=r²相切，则半径r的值是

A.　　　　　　　　　　　　 B.　　　　　　　　　　　　　C. 　　　　　　　　　　　　　　D.1

4.复数z满足arg（z+2）=，则z－2的最小值是

A.1　　  　　　　　　　　　　B.2　　　　　　　　　　　　　C.2　　  　　　　　　　D.2

5.等差数列{a_n}的前n项和为S_n，若a₃+a₁₇=10，则S₁₉的值

A.是55　　　　　　　　　　B.是95　　　　　　　　　　　　C.是100　　　　　　　　　D.不能确定

6.过定点P（0，2）作直线l，使l与曲线y²=4（x－1）有且仅有1个公共点，这样的直线l共有

A.1条　　　　　　　　　　 B.2条　　　　　　　　　　　C.3条　　　　　　　　　　 D.4条

7.某产品的总成本y（万元）与产量x（台）之间的函数关系式是y=3000+20x－0.1x²（0<x<240，x∈N），若每台产品的售价为25万元，则生产者不亏本时（销售收入不小于总成本）的最低产量是

A.100台　　　　　　　　　B.120台　 　　　　　　 C.150台　　 　　　　 D.180台

8.对于已知直线a，如果直线b同时满足下列三个条件：①与a是异面直线；②与a所成的角为定值θ；③与a的距离为定值d.那么，这样的直线b有

A.1条　　　　　　　　　　 B.2条　　　　　　　　　　　　　C.3条　　　　　　　 D.无数条

9.某学生计划有不超过10元的钱购买单价分别为0.5元、0.6元的铅笔和练习本.根据需要，铅笔至少买7支，练习本至少买6本，则不同的选购方式共有

A.10　　  　　　　　　　　　B.15　　　　　　　　　　　　C.19　　　　　　　　  D.20

10.为了使函数y=sinωx（ω>0）在区间［0，1］上至少出现50次最大值，则ω的最小值是

A.98π　　  　　　　　　　　　　 B.π　　  　　　　　C.π　　  　　 D.100π

11.在f₁（x）=，f₂（x）=x²，f₃（x）=2^x，f₄（x）=logx四个函数中，当x₁>x₂>1时，使［f（x₁）+f（x₂）］<f（）成立的函数是

A.f₁（x）=x　　　　　　　　　　　　　　　　　　　　　　 B.f₂（x）=x²

C.f₃（x）=2^x　　　　　　　　　　　　　　　　　　　　　　　 D.f₄（x）=logx

12.设P（x，y）是曲线C：x²+y²+4x+3=0上任意一点，则的取值范围是

A.［－］　　  　　　　　　　　　　　　　　　　　B.（－∞，－）∪［，+∞］

C.［－］　　  　　　　　　　　　　　　　　　　D.（－∞，－）∪［，+∞］

第Ⅱ卷（非选择题　共90分）

二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）

13.一个凸多面体的面都是四边形，则它的顶点数与面数的差是　　　　  .

14.不等式<1的解集为（－∞ ，1）∪（2，+∞），则a=　　　　.

15.=　　　　　 .

16.已知x∈（0，π），则y=sinx+的最小值为　　　　.

三、解答题（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤）

17.（本小题满分12分）

已知复数z₁=x+ai，z₂=x+bi（b>a>0，x>0）的辐角主值分别为α，β，求tan（β－α）的最大值及对应的x的值.

18.（本小题满分12分）

如图，M—l—N是120°的二面角，A、B两点在棱上，AB=2，D在平面M内，三角形ABD是等腰直角三角形，∠DAB=90°,C在N内,三角形ABC是直角三角形，∠ACB=90°，∠ABC=60°.

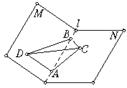
（1）求三棱锥D—ABC的体积；

（2）求直线BD与平面N所成的角的正弦值；

（3）求二面角D—AC—B的平面角的正切值.

19.（本小题满分12分）

一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比.

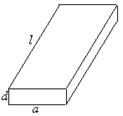
（1）将此枕木翻转90°（即宽度变为了厚度），枕木的安全负荷变大吗？为什么？

（2）现在一根横断面为半圆（半圆的半径为R）的木材，用它来截取成长方形的枕木，其长度即为枕木规定的长度，问如何截取，可使安全负荷最大？

20.（本小题满分12分）

椭圆C₁：=1（a＞b＞0）的左、右顶点分别是A、B，P是双曲线C₂：=1的右支（x轴上方）的一点，线段AP交椭圆于C，PB的延长线交椭圆于D，且C平分AP.

（1）求直线PD的斜率及直线CD的倾斜角；

（2）当双曲线C₂的离心率e为何值时，直线CD恰过椭圆C₁的右焦点.

21.（本小题满分12分）

某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品x（百台），其总成本为G（x）（万元），其中固定成本为2万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本），销售收入R（x）（万元）满足：

R（x）=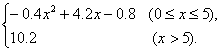

假定该产品产销平衡，那么根据上述统计规律.

（1）要使工厂有赢利，产量x应控制在什么范围？

（2）工厂生产多少台产品时，可使赢利最多？

（3）求赢利最多时每台产品的售价.

22.（本小题满分14分）

设f（x）的定义域为x∈R且x≠，k∈Z，且f（x+1）=－，如果f（x）为奇函数，当0<x<时，f（x）=3^x.

（1）求f（）；

（2）当2k+<x<2k+1（k∈Z）时，求f（x）;

（3）是否存在这样的正整数k，使得当2k+<x<2k+1（k∈Z）时，log₃f（x）>x²－kx－2k有解？

参考答案

一、选择题（每小题5分，共60分）

1.解析：集合P表示正方形，集合Q表示圆面.

答案：A

2.B

3.解析：用d=r去研究线圆相切.

答案：A

4.解析：用数形结合的方法去研究.

答案：D

5.解析：S₁₉=19a₁₀=19·.

答案：B

6.解析：直线l与抛物线相切或与抛物线的对称轴平行.

答案：C

7.C　8.D　9.D

10.解析：由题意1≥49T，其中T为周期.

答案：B

11.解析：研究函数的图象，数形结合，切实理解题中［f（x₁）+f（x₂）］<f（）的意义.

答案：A

12.解析：数形结合，表示点（x，y）与原点连线的斜率.

答案：C

二、填空题（每小题4分，共16分）

13.2　14.　15.333298　16.3

三、解答题（17、18、19、20、21题每题12分，22题14分，共74分）

17.解：由题设知tanα=，tanβ=且0<α<β<，

∴tan（β－α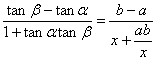）=.　　　　　　　　 5分

∵x>0，>0且x·=ab为定值.

∴当且仅当x=即x=时，x+取得最小值2.

此时tan（β－α）取最大值.　　　　　　　　　　　　　　 12分

18.解：（1）过D向平面N作垂线，垂足为O，连接OA并延长至E.

∵AB⊥AD，OA为DA在平面N内的射影，

∴AB⊥OA.∴∠DAE为二面角M—l—N的平面角.

∴∠DAE=120°.∴∠DAO=60°.

∵AD=AB=2，∴DO=.

∵△ABC是有一个锐角为30°的直角三角形，斜边AB=2，

∴S_△ABC=，又D到平面N的距离DO=.

∴V_D—ABC=.　　　 　　　　　　　　　　　　　　4分

（2）由（1）可知，∠DBO为直线BD与平面N所成的角，

∴sinDBO=.　　　　　　　8分

（3）过O在N内作OF⊥AC，交AC的反向延长线于F，连接DF，则AC⊥DF，

∴∠DFO为二面角D—AC—B的平面角.又在△DOA中，OA=2cos60°=1，即∠OAF=

∠EOC=60°，∴OF=1·sin60°=.

∴tanDFO==2.　　　　　　　　　　　　　12分

19.解：（1）安全负荷y₁=k·（k为正常数），翻转90°后，y₂=k·.

∵，

∴当0<d<a时，y₁<y₂，安全负荷变大；

当0<a<d时，y₂<y₁，安全负荷变小.　　　　 5分

（2）设截取的宽为a，高为d，则（）²+d²=R²，即a²+4d²=4R².

∵枕木长度不变，

∴u=ad²最大时，安全负荷最大.

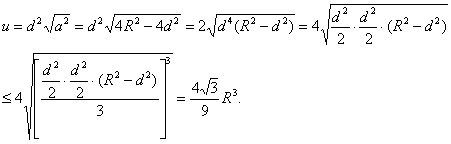
当且仅当=R²－d²，即取d=R，取a=2R时，u最大，即安全负荷最大.　　　　　　　 12分

20.解：（1）由已知A（－a，0），B（a，0），设P（x₀，y₀），C（x₁，y₁），D（x₂，y₂），x₀>a，y₀>0，则.将C（）代入椭圆方程得.

∵=1，消去y₀得x₀=2a或x₀=－a（舍）.将x₀=2a代入双曲线方程得y₀=b，∴P（2a，b）.

∴k_PD=k_PB=.

∴PD的方程为y=（x－a），代入椭圆方程得2x²－3ax+a²=0.

解得x₂=或x₂=a（舍）.

∵x₁=，∴x₁=x₂.

∴CD的倾斜角为90°.　　　　　　　6分

（2）当直线CD过椭圆C₁的右焦点F₂（c，0）时，x₁=x₂=c，则a=2c，∴b=c，即b=a.在双曲线中半焦距c′=a，

∴e=，这时CD恰过椭圆C₁的右焦点.　　　　　　12分

21.解：依题意，G（x）=x+2.设利润函数为f（x），则

f（x）=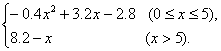

（1）要使工厂有赢利，即解不等式f（x）>0，

当0≤x≤5时，解不等式－0.4x²+3.2x－2.8>0，

即x²－8x+7<0，∴1<x<7.∴1<x≤5;

当x>5时，解不等式8.2－x>0，得x<8.2，∴5<x<8.2.

综上，要使工厂赢利，x应满足1<x<8.2，即产品应控制在大于100台且小于820台的范围.　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　5分

（2）0≤x≤5时，f（x）=－0.4（x－4）²+3.6，故当x=4时，f（x）有最大值3.6，而当x>5时，f（x）<8.2－5=3.2.

所以，当工厂生产400台产品时，赢利最多.　　　　　　　　 9分

（3）即求x=4时的每台产品的售价，

此时售价为=2.4（万元/百台）=240元/台.　　 12分

22.解：（1）∵f（x+2）=－=f（x），

∴f（x）是周期为2的周期函数.

∴.　　　　　　　 5分

（2）∵2k+<x<2k+1，k∈Z，∴<x－2k<1，－<x－2k－1<0，0<2k+1－x<.

∴f（2k+1－x）=3^2k+1－x.

又f（2k+1－x）=f（1－x）=－f（x－1）=－f（x+1）=.

∴f（x）==3^x－2k－1.　　　　　　　　　　　　　10分

（3）∵log₃f（x）>x²－kx－2k，

∴x－2k－1>x²－kx－2k，x²－（k+1）x+1<0（_*）

Δ=k²+2k－3.

①若k>1且k∈Z时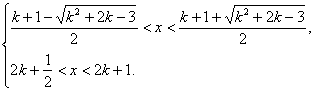

但是

∴x∈.

②若k=1，则Δ=0，（_*）无解.

∴不存在满足条件的整数k.　　　　　　　　　　　　　　14分