高三第二次模拟数学试卷（文科）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页。共150分。考试时间120分钟。
第Ⅰ卷（选择题共50分）
注意事项：
1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。
3. 考试结束，监考人将本试卷和答题卡一并收回。
参考公式：
三角函数的和差化积公式
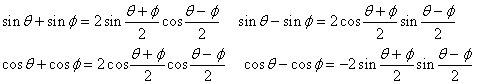
正棱台、圆台的侧面积公式
其中c’，c分别表示上、下底面周长，l表示斜高或母线长
台体的体积公式
其中S’、S分别表示上、下底面积，h表示高
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）已知集合
是从集合A到B的一个映射，若
，则B中的元素3的原象为
（A）—1 （B）1 （C）2 （D）3
（2）已知命题甲为x>0；命题乙为x>0，那么
（A）甲是乙的充分非必要条件
（B）甲是乙的必要非充分条件
（C）甲是乙的充要条件
（D）甲既不是乙的充分条件，也不是乙的必要条件
（3）下列函数中，周期为π的奇函数是
（4）在复平面中，已知点A（2，1），B（0，2），C（-2，1），O（0，0）。给出下面的结论：
①直线OC与直线BA平行； ②
；
③
；
④
。
其中正确结论的个数是
（A）1个 （B）2个 （C）3个 （D）4个
（5）过原点的直线与圆
相切，若切点在第二象限，则该直线的方程是 
（6）在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1：3，则锥体被截面所分成的两部分的体积之比为
（A）
（B）1：9 （C）
（D）
（7）将4张互不相同的彩色照片与3张互不相同的黑白照片排成一排，任何两张黑白照片都不相邻的不同排法的种数是
（A）
（B）
（C）
（D）
（8）已知数列
的通项公式是
，其中a，b均为正常数，那么
的大小关系是
（A）
（B）
（C）
（D）与n的取值相关
（9）双曲线的虚轴长为4，离心率
,
分别是它的左、右焦点，若过
的直线与双曲线的左支交于A，B两点，且AB是
与
的等差中项，则AB等于
（A）
（B）
（C）
（D）8
（10）某农贸市场出售西红柿，当价格上涨时，供给量相应增加，而需求量相应减少，具体调查结果如下表：
表1 市场供给表
| 单价（元/kg） | 2 | 2. 4 | 2. 8 | 3. 2 | 3. 6 | 4 |
| 供给量（1000kg） | 50 | 60 | 70 | 75 | 80 | 90 |
表2 市场需求表
| 单价（元/kg） | 4 | 3. 4 | 2. 9 | 2. 6 | 2. 3 | 2 |
| 需求量（1000kg） | 50 | 60 | 65 | 70 | 75 | 80 |
根据以上提供的信息，市场供需平衡点（即供给量和需求量相等时的单价）应在区间
（A）（2. 3，2. 6）内 （B）（2. 4，2. 6）内
（C）（2. 6，2. 8）内 （D）（2. 8，2. 9）内
第Ⅱ卷（非选择题共100分）
注意事项：
1. 第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中。
2. 答卷前将密封线内的项目填写清楚。
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
|
|
（11）
的值为______。
（12）已知偶函数f（x）的图象与x轴有五个公共点，那么方程f（x）=0的所有实根之和等于_________。
（13）已知抛物线
上一点A到此抛物线的焦点的距离为
，那么点A的坐标为_______。
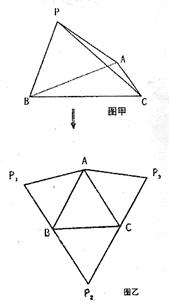
（14）将三棱锥P—ABC（如图甲）沿三条侧棱剪开后，展开成如图乙的形状，其中
共线，
共线，且
，则在三棱锥P—ABC中，PA与BC所成的角的大小是___________。
三、解答题：本大题共6小题，共84分。解答应写出文字说明，证明过程或演算步骤。
（15）（本小题满分13分）
已知
，求tg2x的值。
（16）（本小题满分13分）
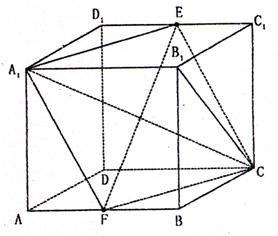
如图，在边长为a的正方体ABCD—
中，E、F分别为
与AB的中点。
（Ⅰ）求证：四边形
是菱形；
（Ⅱ）求证：
（Ⅲ）求
一平面所成角的正切值。
（17）（本小题满分14分）
函数f（x）是定义在（0，+∞）上的减函数，且对一切a，b∈（0，+∞），都有
（Ⅰ）求f（1）的值；
（Ⅱ）若f（4）=1，解不等式
。
（18）（本小题满分14分）
双曲线的中心在原点，焦点在x轴上，且过点（-3，2）。过这个双曲线的右焦点且斜率为
的直线交双曲线的两条准线于M，N两点，以MN为直径的圆过原点，求此双曲线的方程。
（19）（本小题满分15分）
某城市为了改善交通状况，需进行路网改造。已知原有道路a个标段（注：1个标段是指一定长度的机动车道），拟增建x个标段的新路和n个道路交叉口，n与x满足关系n = ax + b，其中b为常数。设新建1个标段道路的平均造价为k万元，新建1个道路交叉口的平均造价是新建1个标段道路的平均造价的β倍（β≥1），n越大，路网越通畅，记路网的堵塞率为μ，它与β的关系为
。
（Ⅰ）写出新建道路交叉口的总造价y（万元）与x的函数关系式：
（Ⅱ）若要求路网的堵塞率介于5%与10%之间，而且新增道路标段为原有道路标段数的25%，求新建的x个标段的总造价与新建道路交叉口的总造价之比P的取值范围；
（Ⅲ）当b = 4时，在（Ⅱ）的假设下，要使路网最通畅，且造价比P最高时，问原有道路标段为多少个？
（20）（本小题满分15分）
已知函数
，其中p > 0，p + q > 1。对于数列，设它的前n项和为
，且
（n∈N）。
（Ⅰ）求数列的通项公式；
（Ⅱ）证明：
；
（Ⅲ）证明：点
…，
都在同一直线上。
数学参考答案及评分标准（文）
一、（1）C （2）A （3）A （4）C （5）D （6）D （7）D
（8）B （9）A （10）C
二、（11）1 （12）0 （13）
（14）90°
三、（15）解：根据倍角公式
由原式得
（16）解：（Ⅰ）取中点G，连结
，GF。
则四边形
是平行四边形。
∴ 
。
同理
。
∴
。
由勾股定理易算出
∴ 四边形是菱形（3分）
（Ⅱ）连结
。
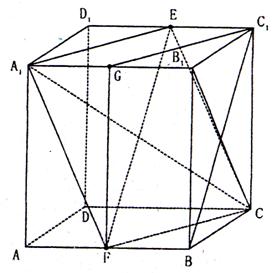
四边形为菱形。∴ 
。（4分）
。
∴ 四边形
为平行四边形。
∴ 
。
。（6分）
则有EF
平面
。（7分）
（Ⅲ）由（Ⅰ）知，EF⊥平面，又EF
平面。
∴平面⊥平面。（8分）
∴
在平面上的射影在线段
上。
∴∠
为与截面所成的角。（10分）
⊥平面
。
∴⊥
。（11分）
在RtΔ中，
，
a。
∴
。
即与截面所成角的正切值为
。（13分）
（17）解：（Ⅰ）令a =b =
1，则
（5分）
（Ⅱ）∵f（4）=1，
∴ 
。①（分）
∴ 
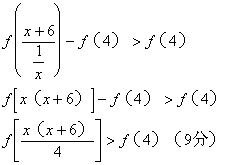
在（0，+∞）上是减函数，
∵①等价于
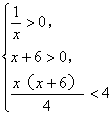
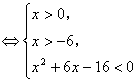
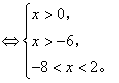（13分）
即有0 < x < 2。（14分）
（18）解：设双曲线方程为
（a>0，b>0）
∵点P（-3，2）在双曲线上，
∴
。①（3分）
设直线
与双曲线两准线方程
联立。
解得M、N坐标为
，
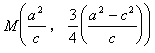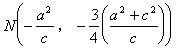（7分）
∵以MN为直径的圆过原点，
∴OM⊥ON，从而
。（9分）
即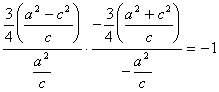
。
解得 
。 ∴
。②（11分）
由①、②解得
。（13分）
故所求双曲线方程为
。（14分）
（19）解：（Ⅰ）依题意得，新建道路交叉口的总造价（单位：万元）为
y = kβn = k β（ax+b）。（5分）
（Ⅱ）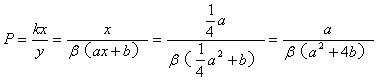
。（7分）
由于 5%≤μ≤10%
有 
则 
∴ 5≤1+β≤10。
∴ 4≤β≤9。（8分）
∴
又由已知P>0，
>0，从而
。
所以P的取值范围是
（无等号不扣分。（10分）
（Ⅲ）当b=4时，在（Ⅱ）的条件下，若路网最通畅，则β=9。
又造价比最高。
∴
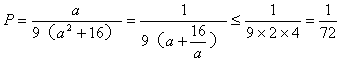。（13分）
当且仅当 
即a=4时取等号。
∴ 根据（Ⅲ）的条件，原有道路标段是4个。（15分）
（20）解：（Ⅰ）∵
∴
。
当n =1时，
；（1分）
当n≥2时，
=（2n-1）p+q。（3分）
由于n=1时，
适合上式，故数列的通项公式为
（n∈N）。（5分）
（Ⅱ）
，
∴
∴是以2p为公差的递增的等差数列。（7分）
即
，而
。（9分）
所以。（10分）
（Ⅲ）要证
在同一直线上，只需证明其中任意一点
与
连线的斜率为定值即可。
∵
∴
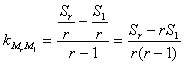
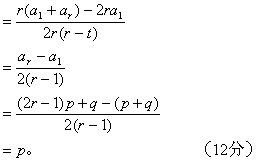
的连线的斜率为定值p，
即都在过
且斜率为p的直线上。
故
。（14分）
| 年级 | 高三 | 学科 | 数学 | 版本 | 期数 | ||||||||
| 内容标题 | 北京市东城区2003年高三第二次模拟数学试卷（文科） | ||||||||||||
| 分类索引号 | G.622.475 | 分类索引描述 | 统考试题与题解 | ||||||||||
| 主题词 | 北京市东城区2003年高三第二次模拟数学试卷（文科） | 栏目名称 | 高考题库 | ||||||||||
| 供稿老师 | 审稿老师 | ||||||||||||
| 录入 | 常艳霞 | 一校 | 康纪云 | 二校 | 审核 | ||||||||