高三复习练习二函数（2）
班级___________ 姓名_____________ 学号____________ 成绩___________
一、选择题：（每小题5分，共50分）
1、已知函数
则
的值为（ ）
（A）9 （B）
（C）-9 （D）
此题7班正答率97.8％,13班正答率100％
2、已知奇函数
是R上的增函数，则
在R上（ ）
（A）既是奇函数又是增函数 （B）既是奇函数又是减函数
（C）既是偶函数又是增函数 （D）既是偶函数又是减函数
此题7班正答率93.5％,13班正答率95.6％
3、若函数f(x)的图像与
的图像关于y=x对称，则f(2x-x2)的单调递增区间是（ ）
（A）[1，+∞] B、[1，2] C、（0，1） D、（-∞，1）
此题7班正答率78.3％,13班正答率80.0％
4、已知函数
，集合
，且
，则实数a的取值范围是（ ）
（A）（0，+∞）（B）（2，+∞） （C）[4，+∞] （D）（-∞，0）∪[4，+∞]
此题7班正答率17.4％,13班正答率66.7％
5、已知函数y=f(x)在（-3，0）上是减函数，且y=f(x-3)是偶函数，则下列结论正确的是（ ）
（A）
（B）
（C）
（D）
此题7班正答率73.9％,13班正答率80.0％
6、若0＜a＜1，则函数
在定义域上是（ ）
（A）增函数且y＞0 （B）增函数且y＜0
（C）减函数且y＞0 （D）减函数且y＜0
此题7班正答率84.8％,13班正答率97.8％
7、将进货单价为80元的商品按90元一个售出时，能卖出400个，已知该商品每个涨价1元，其销售就减少20个，为了获得最大利润，售价应定为每个（ ）
（A）110元 （B）105元 （C）100元 （D）95元
此题7班正答率84.8％,13班正答率97.8％
8、二次函数f(x)满足f(2+x)=f(2-x)，又f(x)在[0，2]上单调递增，且f(a)≥f(0)，则实数a的取值范围是（ ）
（A）a≥2 （B）a＜0 （C）0≤a≤4 （D）a＜0或a≥4
此题7班正答率93.5％,13班正答率100％
9、已知函数y=f(x)的反函数为
，现将函数y=f(3-2x)的图像向左平移1个单位，向上平移2个单位，再关于原点对称后所得函数的反函数为（ ）
（A）
（B）
此题7班正答率58.7％,13班正答率68.9％
（C）
（D）
10、设f(x)是定义在R上的偶函数，且对任意的x都有f(x-1)=f(x+3),在区间[4，6]上，f(x)=2x+1,则在区间[-2，0]上f(x)的反函数为（ ）
（A）
（B）
此题7班正答率47.8％,13班正答率95.6％
（C）
（D）
二、填空题：（每小题4分，共16分）
11、若关于x的方程x2 +2ax+a+1=0一根比2大，另一根比2小，则实数a的取值范围是_____________
12、若幂函数
的图像与x轴，y轴都不相交，且图像关于y轴对称，则m的值为___________ （此题学生出错特多）
13、函数
的反函数的定义域为____________
14、若函数
在区间
上递减，则实数a的取值范围是______________
（此题学生出错特多）
三、解答题：（第15、16题各10分，第17题14分）
15、比较
与
的大小（要写出过程）
16、某工厂生产容积为
立方米的圆柱形无盖容器，制造底面的材料每平方米30元，制造侧面的材料每平方米20元，设计时，材料的厚度及损耗可忽略不计。
（1）把制造容器的成本y（元）表示成容器底面半径x（米）的函数；
（2）设a，b∈R+，且a＜b，x在区间[a，b]内变动，在a=0.5，b=5时求出最低成本是多少元？（精确到1元）
练习（1）答案（理科普通班平均75分，实验班平均101分）
ACAAC BDACD 11. –1; 12. 1-2a; 13. ①; 14. –6; 15. a=1,b=1,c=0;
16. 
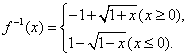17.(1)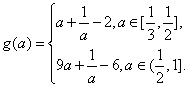 
(2) g(
)在[
] 上是单调递减的函数；在[
] 上是单调递增的函数。
所以，当
时，g()有最小值
。
18．
练习（2）答案（理科普通班平均59.1分，实验班平均77.2分）
BBBAD CDCDA 11. 
; 12. –1,1,3; 13. (-1,0); 14.[
]
15. （作差比较法）当
时，
；
当
时，
；当
时，
.
16. (1) 
; (2) 
(元)。
17．（1）
在[-1，1]上是增函数。利用定义证明：任取
，
则
；即
。
（2）
；（3）等转化为
在
[-1，1]上恒成立，有以下三种解法。
解法1：令
，则必须有
；
解法2：当
时符合题意；当
；当
。
解法3：
取交集便得。
17、已知f(x)是定义在[-1，1]上的奇函数，且f(1)=1,若a,b∈[-1,1]，a+b≠0,有
（1）判断f(x)是[-1,1]上是增函数，还是减函数，并证明你的结论；
（2）解不等式
；
（3）若f(x)≤m2-2am+1对所有的x∈[-1,1],a∈[-1,1]恒成立，求实数m的取值范围。