高三年级数学试题

高三年级数学试题

参考公式：三角函数的积化和差公式

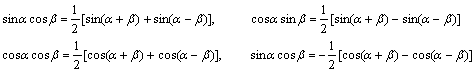
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)

1.设集合M={x0≤x＜2则集合等于

A. {x0≤x＜1　　  B.{ x0≤x＜2　　 C.{x0≤x≤1}　　　D.{ x0≤x≤2}

2.将y=2^x 的图象

A.先向左平行移动1个单位　　　　　　 B.先向右平行移动1个单位

C.先向上平行移动1个单位　　　　　　 D.先向下平行移动1个单位

再作关于直线y=x 对称的图象,可得到函数y=log₂(x+1)的图象.

3.函数的最小正周期是

A.　　　　　　  B.　　　　　　  C.2　　　　　 　 D.4

4 .(理)函数≤x≤0）的反函数是

A.( 0≤x≤2)　　　　  B.(0≤x≤2)

C. ( 0≤x≤2)　　　　　D. (0≤x≤2)

　 (文)函数的反函数是

A.　　　　　　 B.

C.　　　　　　 D.

5.在等比数列{a_n}中,a₁>1,前n项和S_n满足那么a₁的取值范围是

A.(1,)　　　　  B.(1,4)　　　　 　 C.(1,2)　　　　　　 D.(1,)

6.不等式组　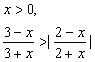的解集是

A.{x0<x<2}　　　　B.{x0<x<2.5}　　　 C.{x0<x<}　　　D.{x0<x<3}

7.有一长度为10m的直椭圆柱形的储油罐,其横断面是如下图所示的椭圆,则该储油罐的容积不可能是

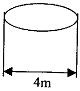
A.25　　　　　　　　　　　 　　　B.30

C.35　　　　　　　　　　　 　　　D.40

8.在(1－x³)(1+x)¹⁰的展开式中, x⁵的系数是

A.－297　　　　 　 B.－252　　　　　 C.297　　　　　 　 D.207

9.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为

A.120°　　　　 　 B.150°　　　　　 C.180°　　　　 　 D.240°

10四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同取法共有

A.150种　　　　 　 B.147种　　　 　 C.144种　　　　 　 D.141种

11.直线截圆x²+y²=4所得的劣弧所对的圆心角为

A.　　　　　  　 B.　　　　  　 C.　　　　　　 　D.

12.若椭圆经过原点,且焦点为F₁(1,0),F₂(3,0),则其离心率为

A.　　　　　  　 B.　　　　　 　 C.　　　　　  　 D.

二、填空题(本大题共6小题,每小题4分,共24分,把答案填在题中横线上.)

13.甲、乙两人同时从图书馆走向教室.甲一半路程步行一半路程跑步；乙一半时间步行一半时间跑步.如果两人步行速度、跑步速度分别相同,那么先到教室的应该是　　　　 .

14.与椭圆关于直线x＋y=0对称的椭圆的方程是　　　　.

15.设a、b是两个实数,给出下列条件：① a＋b>1; ② a＋b=2; ③ a＋b>2;

④a²＋b²>2; ⑤ ab>1.其中能推出“a、b中至少有一个大于1”的条件是　　　 .

　　(注: 把你认为满足要求的条件的序号都填上.)

16.设函数f (x)=ax²+bx+c (a≠0),对任意实数t都有f (2＋t)=f (2－t)成立.在函数值f (－1)、f(1)、f (2)、f (5) 中,最小的一个不可能是　　　　.

17.对于任意定义在R上的函数f (x) ,若实数x₀满足f (x₀) =x₀,则称x₀是函数f (x)的一个不动点.若函数f (x) =x²＋ax＋1没有不动点,则实数a的取值范围是　　　　 .

18.已知函数f (x)=x²＋ax＋b－3 (xR) 的图象恒过点(2,0),则a²＋b²的最小值为　　　　 .

三、解答题(本大题共6小题,共66分.解答应写出文字说明,证明过程或演算步骤)

19.(本小题满分8分)

已知关于x的方程,其中a、b为实数.

(1)　  若x=(i为虚数单位)是该方程的根,求a、b的值；

(2)　  当时, 证明该方程没有实数根.

20. (本小题满分10分)

已知f (x)=2cos²x＋sin2x＋a (aR为常数) .

(1)　  若xR,求f (x)的单调递增区间;

(2)　  若时, f (x)的最大值为4,求a的值.

21.(本题满分12分)

若f (x)是定义在(0,)上的增函数,且对一切x>0,满足f

(1)求f (x)的值;　 (2) 若f (6)=1,解不等式

22.(本小题满分10分)

某俱乐部准备承办一场足球赛,预计共卖出门票2.4万张,票价有3元、5元、8元三种,

且票价3元和5元的张数之积为0.6万.设x是门票的总收入,经预算,扣除各项支出后,该俱乐部的纯收入函数为y=lg2^x.试问三种门票分别为多少张时,纯收入最高?

23.(本小题满分12分)

已知二次函数f (x)=ax²＋bx (a, b为常数,且a≠0)满足条件:f (－x＋5)=f (x－3),且方程

f (x)=x有等根.

(1)　  求f (x)的解析式;

(2)　  是否存在m、n(m<n),使f (x)的定义域和值域分别为[m, n]和[3m,3n]?如果存在,求出

m、n的值;如不存在,说明理由.

24 .(本小题满分14分)

数列{a_n}、{b_n}分别是无穷等差、等比数列,数列{a_n}的前n项和,数列{b_n}中, b₃=4, b₆=32.

(1)　  求数列{a_n}和{b_n}的通项公式;

(2)求数列的所有项之和;

(3)记{c_n}(n)是数列{a_n}和{b_n}的所有相同项(排列顺序不变)组成的数列,求{c_n}的

通项公式.