三角
一)选择题
1. (2004.江苏)函数y=2cos2x+1(x∈R)的最小正周期为 ( B)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.(2004.全国理)为了得到函数![]() 的图象,可以将函数
的图象,可以将函数![]() 的图象 ( B )
的图象 ( B )
A.向右平移![]() 个单位长度 B.向右平移
个单位长度 B.向右平移![]() 个单位长度
个单位长度
C.向左平移![]() 个单位长度 D.向左平移
个单位长度 D.向左平移![]() 个单位长度
个单位长度
3、(2004.上海理)三角方程2sin(![]() -x)=1的解集为( C
)
-x)=1的解集为( C
)
(A){x│x=2kπ+![]() ,k∈Z}. (B)
{x│x=2kπ+
,k∈Z}. (B)
{x│x=2kπ+![]() ,k∈Z}.
,k∈Z}.
(C) {x│x=2kπ±![]() ,k∈Z}. (D)
{x│x=kπ+(-1)K,k∈Z}.
,k∈Z}. (D)
{x│x=kπ+(-1)K,k∈Z}.
4.(2004.湖北理)设![]() 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中![]() .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数![]() 的图象可以近似地看成函数
的图象可以近似地看成函数![]() 的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是 ( A )
的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是 ( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.(2004. 福建理)tan15°+cot15°的值是 ( C )
A.2 B.2+![]() C.4 D.
C.4 D.![]()
6.(2004. 重庆理)![]() ( B )
( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(2004. 辽宁卷)若![]() 的终边所在象限是D
的终边所在象限是D
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.(2004. 辽宁卷)已知函数![]() ,则下列命题正确的是B
,则下列命题正确的是B
A.![]() 是周期为1的奇函数 B.
是周期为1的奇函数 B.![]() 是周期为2的偶函数
是周期为2的偶函数
C.![]() 是周期为1的非奇非偶函数 D.
是周期为1的非奇非偶函数 D.![]() 是周期为2的非奇非偶函数
是周期为2的非奇非偶函数
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10、(2004. 人教版理科)函数![]() 的最小正周期是( )
的最小正周期是( )
A、 ![]() B、
B、 ![]() C、
C、![]() D、
D、![]()
11、(2004. 人教版理科)在△ABC中,AB=3,BC=![]() ,AC=4,则边AC上的高为( )
,AC=4,则边AC上的高为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、(2004. 四川理)已知函数y=tan(2x+φ)的图象过点(![]() ),则φ的值可以是( A )
),则φ的值可以是( A )
A -![]() B
B ![]() C
C
![]() D
D
![]()
13、(2004. 四川理)函数y=xcosx-sinx在下面哪个区间内是增函数( B )
A (![]() ) B (π,2π) C (
) B (π,2π) C (![]() ) D (2π,3π)
) D (2π,3π)
14、(2004. 四川理)函数y=sin4x+cos2x的最小正周期为( B )
A ![]() B
B
![]() C
π
D 2π
C
π
D 2π
15. (2004. 天津卷)函数![]() )为增函数的区间是(C )
)为增函数的区间是(C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
`16.(04.上海春季高考)下列函数中,周期为1的奇函数是 ( D )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二)填空题
17.(04. 上海春季高考)在![]() 中,
中,![]() 分别是
分别是![]() 、
、![]() 、
、![]() 所对的边。若
所对的边。若![]() ,
,![]() ,
,![]() ,
则
,
则![]() __________.2
__________.2
18、(2004. 人教版理科)函数![]() 在区间
在区间![]() 上的最小值为
.
上的最小值为
.
19、(2004. 上海卷文科)若tgα=![]() ,则tg(α+
,则tg(α+![]() )= 3 .
)= 3 .
三)解答题
20.(2004. 辽宁卷)(本小题满分12分)
设全集U=R
(1)解关于x的不等式![]()
|
若( ∪A)∩B恰有3个元素,求a的取值范围.
20.本小题主要考查集合的有关概念,含绝对值的不等式,简单三角函数式的化简和已知三
角函数值求角等基础知识,考查简单的分类讨论方法,以及分析问题和推理计算能力. 满
分12分.
解:(1)由![]()
当![]() 时,解集是R;
时,解集是R;
当![]() 时,解集是
时,解集是![]() ……………………3分
……………………3分
|
|
因![]()
![]()
由![]() …………8分
…………8分
|
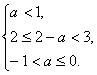 解得
解得21.(2004.湖南理)(本小题满分12分)
已知![]() 的值.
的值.
21.解:由![]()
![]()
得 ![]() 又
又![]()
于是 ![]()
![]()
22.(2004. 天津卷)(本小题满分12分)
已知![]()
(I)求![]() 的值;
的值;
(II)
(2004. 天津卷)求![]() 的值。
的值。
22.本小题考查两角和正切公式,倍角的正弦、余弦公式等基础知识,考查运算能力.满分12分.
解:
(I)解: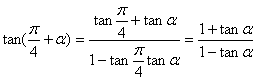
由 ![]() ,有
,有
![]()
解得 ![]() 。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。4分
(II)解法一:![]() 。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。6分
![]()
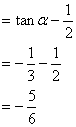 。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。12分
解法二:由(I),![]() ,得
,得![]()
![]()
![]()
![]()
![]()
![]() 。。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。。6分
于是 ![]() 。。。。。。。。。。。。。。。。。。。。。。。8分
。。。。。。。。。。。。。。。。。。。。。。。8分
![]() 。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。10分
代入得
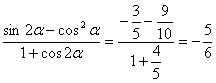 。。。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。。。12分
23.(2004.江苏)已知0<α<![]() ,tan
,tan![]() +cot
+cot![]() =
=![]() ,求sin(
,求sin(![]() )的值.
)的值.
23、解:由题意可知![]() ,
,
![]()
24.(2004. 福建理)(本小题满分12分)
设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,
![]() sin2x),x∈R.
sin2x),x∈R.
(Ⅰ)若f(x)=1-![]() 且x∈[-
且x∈[-![]() ,
,![]() ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量c=(m,n)(m<![]() )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
24. 本小题主要考查平面向量的概念和计算,三角函数的恒等变换及其图象变换的基本技能,考查运算能力.满分12分.
解:(Ⅰ)依题设,f(x)=2cos2x+![]() sin2x=1+2sin(2x+
sin2x=1+2sin(2x+![]() ).
).
由1+2sin(2x+![]() )=1-
)=1-![]() ,得sin(2 x +
,得sin(2 x +![]() )=-
)=-![]() .
.
∵-![]() ≤x≤
≤x≤![]() ,∴-
,∴-![]() ≤2x+
≤2x+![]() ≤
≤![]() ,∴2x+
,∴2x+![]() =-
=-![]() ,
,
即x=-![]() .
.
(Ⅱ)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(Ⅰ)得 f(x)=2sin2(x+![]() )+1.
)+1.
∵m<![]() ,∴m=-
,∴m=-![]() ,n=1.
,n=1.
25.(2004.湖北理)(本小题满分12分)
已知![]() 的值.
的值.
25.本小题考三角函数的基本公式以及三角函数式的恒等变形等基础知识和基本运算技能,满分12分.
解法一:由已知得:![]()
![]()
由已知条件可知![]()
![]()
![]()
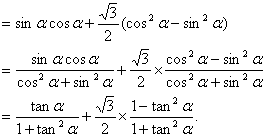
![]()
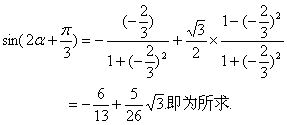
解法二:由已知条件可知![]()