数学高考模拟试题2
一、选择题（每小题5分，共60分）
1．已知集合
和
，若
，则实数m取值的个数为（ ）．
A．0 B．1 C．2 D．3
2．函数
的最小正周期和最大值分别是（ ）．
A．
与
B．与2 C．4与 D．4与2
3．今有一组实验数据如下：
| x | 1.993 | 3.002 | 4.001 | 5.032 | 6.121 |
| y | 1.501 | 4.041 | 7.498 | 12.04 | 17.93 |
现准备用下列函数中的一个近似地表示数据满足的规律，其中最接近的一个是（ ）．
A．
B．y＝2x-2
C．
D．
4．已知三条直线m、n、l和三个平面
、
、
，有下面四个命题：
①m⊥l，
②m⊥，
③⊥l，
④
，
其中正确的两个命题是（ ）．
A．①与② B．②与③ C．③与④ D．④与①
5．在极坐标系中，经过点（2，
）且垂直于极轴的直线的极坐标方程是（ ）．
A．
B．
C．
D．
6．把曲线
先沿x轴向右平移
个单位，再沿y轴向下平移1个单位，得到的曲线方程是（ ）．
A．（1-y）sin x＋2y-1＝0 B．（y-1）sin x＋2y-1＝0
C．（y＋1）sin x＋2y＋3＝0 D．-（y＋1）sin x＋2y＋3＝0
7．已知
、
是椭圆
＜b＜
的两个焦点，B是短轴的一个端点，则△
的面积的最大值为（ ）．
A．1 B．2 C．3 D．4
8．甲、乙两工厂2002年元月份的产值相等，甲厂的产值逐月增加，且每月增加的产值相同；乙厂的产值也逐月增加，且每月增长的百分率相同．若已知2003年元月份两厂的产值也相等，则2002年7月份甲、乙两厂的产值
和
的关系是（ ）．
A．＞ B．＝
C．＜ D．不能确定
9．函数
与函数
的图象关于直线l对称，则直线l的方程是（ ）．
A．x＝0 B．y＝0
C．x-y＝0 D．x＋y＝0
10．如果
是第一象限的角，那么（ ）．
A．
且
B．
且
C．且 D．且
11．已知x、y是两个不等的正数，则
，
，
的大小顺序是（ ）．
A．
B．
C．
D．
12．有8个人分乘两辆不同的车，每辆车最多可坐5个人，则不同的乘车方法数共有（ ）．
A．91种 B．126种 C．182种 D．252种
二、填空题（每小题4分，共16分）
13．设
是首项为2的正数数列，且点（
，
）在双曲线
上（n＝1，2，…），则它的通项公式是＝________．
14．圆锥的轴截面为正三角形，母线长为12，当圆锥的内接圆柱的体积最大时，该内接圆柱的高等于________．
15．若
（n为正整数）的展开式中所有项的系数之和为625，则它的展开式中
的系数是________（用数字作答）．
16．抛物线
的准线与双曲线
的右准线重合，则p＝________．
三、解答题（第17～21题每题12分，第22题14分，共74分）
17．设复数z与
，
满足条件：
，
，
．
（1）已知
，
，r＞0，求复数的三角形式；
（2）试求函数
的最大值以及对应的复数z．
18．如图，在三棱台
中，已知
，
，AB＝3，
，且二面角
为60°．
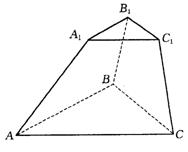
（1）求证：平面ABC⊥平面
；
（2）求三棱锥
的体积；
（3）求二面角
的大小．
19．已知正数数列与
满足：
且
（n＝1，2，…），其中a＞0为常数．
（1）求证：是等比数列；
（2）设
，如果
存在，试求a的取值范围．
20．西部某地区因交通问题严重制约经济发展，某种产品只能在本地销售，每年投资x万元，所获利润为
（万元）．在实施西部大开发战略中，当地政府拟开发此种产品．开发前后，财政预算每年均可投入专项资金60万元．要开发此产品，需先用5年时间每年从60万元专项资金中拿出30万元修通公路（剩余的专项资金仍用于本地销售的投资）．公路修通后该产品可在异地销售，每投资x万元，可获利润：
（万元）．问从10年的总利润来看，该项目有无开发价值?
21．设函数f（x）的定义域为（-1，1），且满足：①对任意的x，y
（-1，1）都有
；②当x（-1，0）时，有f（x）＞0．
（1）求f（0）的值并判断f（x）的奇偶性；
（2）求证：f（x）在（0，1）上是减函数；
（3）设
（n＝0，1，2，…），
（n＝1，2，…），计算
与
的值，由此概括出关于数列，的一个恒等式，并加以证明．
22．设点P为椭圆C：
（a＞b＞0）上任意一点，、为其两个焦点且∠
的最大值为120°．
（1）求椭圆C的离心率；
（2）设过动点
，
的直线l与椭圆C相交于M、N两点，若OQ⊥l且
的最大值为6，试求椭圆C的方程．
参考答案
1．C 2．D 3．C 4．B 5．A 6．C 7．B 8．A 9．D 10．C
11．B 12．C 13．
14．
15．-864 16．2
17．（1）因为，r＞0，于是
．因为，，所以
，从而
．所以
． （2）由及，的三角形式可得：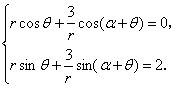
两式平方相加得：
，即
．利用平均不等式：
．故
，
．上式等号成立当且仅当
，即
．此时
，由此可得
＝1，
，从而
．因此的最大值为
，此时
18．（1）连接
，在三棱台
中，因为
，
，又，，所以
，AB⊥BC．而
，所以AB⊥平面．又
平面ABC，故平面ABC⊥平面． （2）因为AB⊥平面，
平面，所以AB⊥，又AB⊥BC，所以∠为二面角的平面角，所以∠＝60°．在Rt△ABC与Rt△
中，由题设及勾股定理可得
，因此△为等边三角形．故
．
（3）设D为BC的中点，连接
，则⊥BC．又AB⊥平面，从而⊥AB，故⊥平面ABC．过D作DE⊥AC于E，连接
．由三垂线定理得：⊥AC，所以∠
为二面角的平面角．所以
，
，从而
，所以二面角的大小为
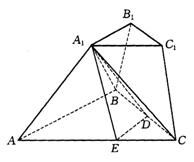
19．（1）由题设可得
．设
，则q是一元二次方程
的正根，所以
．因为a＞0为常数，所以
为常数，故数列是公比的等比数列． （2）由已知，因此是公比为
的等比数列．因为存在，所以
．当
时，上式显然成立．当a＞
时，上式两边平方，解得0＜a＜2，从而＜a＜2．综上所得，所求a的范围是0＜a＜2
20．（1）该产品未开发时，由知，当x＝40时，
．即每年只需从60万元专项资金中拿出40万元投资，可获最大利润10万元．这样10年的总利润最大值为
＝10×10＝100（万元）． （2）该产品开发时，前5年可用于该产品的投资为每年30万元，而f（x）在（0，
上递增，所以
．前5年总利润的最大值
（万元）．设后5年每年x万元用于本地销售投资，60-x万元用于异地销售投资，则后5年总利润为
．当x＝30时，
（万元）．所以10年总利润的最大值为
（万元）．由于
，故该项目具有极大的开发价值
21．（1）在条件（1）中令x＝y＝0可得
，故
．再在（1）中令
（-1，1），得
，即
．所以
为奇函数． （2）设
，由条件①及上述结论可得
……
，因为，所以
，
．所以
（因为
）……
，由条件②及、可知，
，即
．所以在（0，1）上为减函数． （3）因为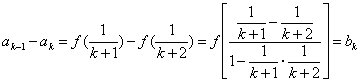
（k＝1，2，…）……
，所以
，
，即
，
．由此猜想：
（n＝1，2，…）……（*）．在ⅲ中令k＝1，2，…，n，相加即得：
．故（*）得证（也可用数学归纳法来证明）
22．（1）在△中，记△
，由余弦定理得
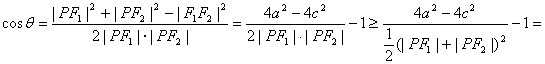
．等号成立当且仅当
．故
的最小值为
120°．解得
． （2）由题设MN的方程为：
…… ①，由得
，椭圆C的方程可化为
…… ②，将①代入②得
．即
．设M（
，
），N（
，
），则由韦达定理得
，
，所以
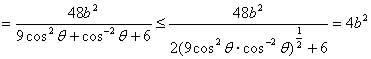．等号成立当且仅当
，即
．所以
，b＝3，从而a＝6．故所求椭圆C的方程为
．