数学高考模拟试题
一、选择题(每小题5分,共60分)
1.已知等差数列![]() 的公差是2,且
的公差是2,且![]() ,则
,则![]()
![]() 等于( ).
等于( ).
A.25 B.50 C.75 D.100
2.已知![]() 、
、![]() 为锐角,且
为锐角,且![]() ,则
,则![]() 等于( ).
等于( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() 、
、![]() 是椭圆
是椭圆![]() 的两个焦点,过
的两个焦点,过![]() 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若![]() ,则
,则![]() 等于( ).
等于( ).
A.11 B.10 C.9 D.16
4.![]() =( ).
=( ).
A.0 B.![]() C.1 D.
C.1 D.![]()
5.已知二面角![]() 的平面角是锐角
的平面角是锐角![]() ,
,![]() 内一点C到
内一点C到![]() 的距离为3,点C到棱AB的距离为4,则
的距离为3,点C到棱AB的距离为4,则![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知函数f(x)是定义在R上的奇函数,当x<0时,![]() ,则
,则![]() 等于( ).
等于( ).
A.-2 B.2 C.![]() D.
D.![]()
7.若双曲线![]() 的焦距为6,则实数m的值为( ).
的焦距为6,则实数m的值为( ).
A.1 B.±1 C.±4 D.4
8.系统抽样又称为等距抽样.从N个个体中抽取n个个体为样本,先将总体中的N个个体编号1,2,3,…,N,再确定抽样间隔,即抽样距![]() (
(![]() 表示
表示![]() 的整数部分).从第一段1,2,…,k个号码中随机抽取一个入样号码
的整数部分).从第一段1,2,…,k个号码中随机抽取一个入样号码![]() ,则
,则![]() ,
,![]() ,…,
,…,![]() 号码均入样构成样本.依此抽样,则每个个体的入样概率( ).
号码均入样构成样本.依此抽样,则每个个体的入样概率( ).
A.相等 B.不相等 C.与![]() 有关 D.与编号有关
有关 D.与编号有关
9.设坐标原点为O,抛物线![]() 与过焦点的直线交于A、B两点,则
与过焦点的直线交于A、B两点,则![]() 等于( ).
等于( ).
A.![]() B.
B.![]() C.3 D.-3
C.3 D.-3
10.甲、乙两乒乓球队各有运动员三男二女,其中甲队一男与乙队一女是种子选手,现在两队进行混合双打比赛,则两个种子选手都上场的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.不等式组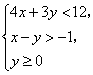 表示的平面区域内,横、纵坐标都是整数的点(x,y)有( ).
表示的平面区域内,横、纵坐标都是整数的点(x,y)有( ).
A.2个 B.4个 C.5个 D.8个
12.如下图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系表示的图象只可能是( ).
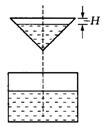
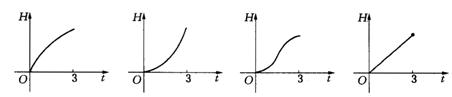
A. B. C. D.
二、填空题(每小题4分,共16分)
13.一个长方体共一顶点的三个面的面积分别为![]() ,
,![]() ,
,![]() ,且它的八个顶点都在同一个球面上,则这个球的面积为_____________.
,且它的八个顶点都在同一个球面上,则这个球的面积为_____________.
14.已知f(x)是定义域为R,最小正周期为![]() 的函数,且当
的函数,且当![]() [
[![]() ,
,![]() ]时,
]时,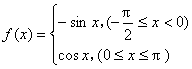 若
若![]() ,则x=_________________.
,则x=_________________.
15.已知数列![]() 的通项公式为
的通项公式为![]() (n=1,2,3,…),且
(n=1,2,3,…),且![]() 满足
满足![]() ,则实数
,则实数![]() 的取值范围是_________________.
的取值范围是_________________.
16.所谓迭代,可以看作同一个运算或操作多次重复.如,自然数的乘法a×k,即k个a累加![]() 可以看作加法运算或函数
可以看作加法运算或函数![]() 的迭代.同样,乘方也可以理解为迭代.又如,等差数列、等比数列的通项公式也是迭代产生的.据此,在生态学中研究的昆虫种群量模式
的迭代.同样,乘方也可以理解为迭代.又如,等差数列、等比数列的通项公式也是迭代产生的.据此,在生态学中研究的昆虫种群量模式![]() ,
,![]() 可以看作函数f(x)=________的迭代.
可以看作函数f(x)=________的迭代.
三、解答题(第17~21题每题12分,第22题14分,共74分)
17.已知函数![]() ,
,![]() 为奇函数,其图象关于直线
为奇函数,其图象关于直线![]() 对称,且在区间
对称,且在区间![]() ,
,![]() 上f(x)为单调函数.求
上f(x)为单调函数.求![]() 和
和![]() 的值.
的值.
18.某新工艺流程如投产成功可收益300万元.但投产之前,必须经过小型试验和中型试验,试验经费分别需2万元和36万元.小型试验的成功率为0.7,如果连做两次小型试验,则成功率可提高到0.8,在小型试验基础上的中型试验的成功率为0.7,如果直接搞中型试验的成功率为0.5.
(1)计算决策甲:先进行一次小型试验,再进行一次中型试验时工程投资获益的期望值.(注:先填写下列表格,再计算其期望值)
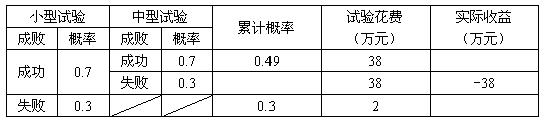
(2)分别计算决策乙和丙工程投资获益的期望值:
决策乙:先进行两次小型试验,再进行一次中型试验.
决策丙:直接进行一次中型试验.
(3)甲、乙、丙三种决策方案中,哪一种决策方案最有利?
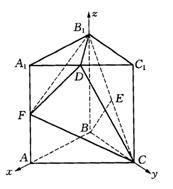
19.如图,在直三棱柱![]() 中,AB=BC,AB⊥BC,且AC=
中,AB=BC,AB⊥BC,且AC=![]() =2,D为
=2,D为![]() 的中点,E为
的中点,E为![]() 的中点.
的中点.
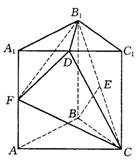
(1)求异面直线BE与DC所成的角;
(2)在线段![]() 上是否存在点F,使CF⊥平面
上是否存在点F,使CF⊥平面![]() ?若存在,求出
?若存在,求出![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)若F为![]() 的中点,求点C到平面
的中点,求点C到平面![]() 的距离.
的距离.
20.已知函数![]() ,(其中a、b为常数,且
,(其中a、b为常数,且![]()
![]() )在区间[-1,1]上的最大值为1,最小值为
)在区间[-1,1]上的最大值为1,最小值为![]() .求a、b的值.
.求a、b的值.
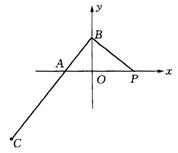
21.如图,已知点P(3,0),点A、B分别在x轴负半轴和y轴上,且![]() ,
,![]() .当点B在y轴上移动时,记点C的轨迹为E.
.当点B在y轴上移动时,记点C的轨迹为E.
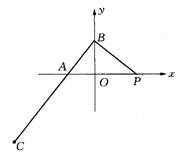
(1)求曲线E的方程;
(2)已知向量![]() =(1,0),
=(1,0),![]() =(0,1),过点Q(1,0)且以向量
=(0,1),过点Q(1,0)且以向量![]() 为方向向量的直线l交曲线E于M、N两点.若D(-1,0),且
为方向向量的直线l交曲线E于M、N两点.若D(-1,0),且![]() ,求t的取值范围.
,求t的取值范围.
22.在xOy平面上有一系列点![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,对每个正整数n,点
,…,对每个正整数n,点![]() 位于函数
位于函数![]() 的图象上,以点
的图象上,以点![]() 为圆心的圆
为圆心的圆![]() 与x轴都相切,且圆
与x轴都相切,且圆![]() 与圆
与圆![]() 又彼此相外切.若
又彼此相外切.若![]() ,且
,且![]() (n=1,2,3,…).
(n=1,2,3,…).
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设圆![]() 的面积为
的面积为![]() ,
,![]() ,求证:
,求证:![]() .
.
参考答案
1.D 2.D 3.A 4.D 5.C 6.B 7.B 8.A 9.B 10.A 11.C 12.B 13.![]() 14.
14.![]() 15.(-3,+∞)
15.(-3,+∞)
16.![]()
17.由![]() 为奇函数知,
为奇函数知,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() .由f(x)图象关于直线
.由f(x)图象关于直线![]() 对称知,
对称知,![]() ,
,![]() .因为
.因为![]() ,所以
,所以![]() ,且
,且![]() ,因为
,因为![]() 在
在![]() ,
,![]() 上为单调函数,所以
上为单调函数,所以![]() ,
,![]() .所以
.所以![]() ,
,![]()
18.(1)填表如下:
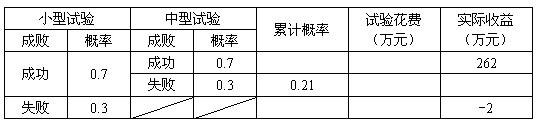
决策甲工程投资获益的期望值为![]() =0.49×262+0.21×(-38)+0.3×(-2)=119.8万元. (2)决策乙工程投资获益的期望值为
=0.49×262+0.21×(-38)+0.3×(-2)=119.8万元. (2)决策乙工程投资获益的期望值为![]() =0.56×260+0.24×(-40)+0.2×(-4)=135.2万元.决策丙工程投资获益的期望值为
=0.56×260+0.24×(-40)+0.2×(-4)=135.2万元.决策丙工程投资获益的期望值为![]() =0.5×264+0.5×(-36)=114万元. (3)由
=0.5×264+0.5×(-36)=114万元. (3)由![]() ,
,![]() 知,决策乙最有利
知,决策乙最有利
19.(1)如图,以B为坐标原点,射线BA、BC、![]() 为x、y、z轴正半轴建立空间直角坐标系.由条件知,B(0,0,0),A(
为x、y、z轴正半轴建立空间直角坐标系.由条件知,B(0,0,0),A(![]() ,0,0),C(0,
,0,0),C(0,![]() ,0),
,0),![]() (0,
(0,![]() ,2),E(0,
,2),E(0,![]() ,1),
,1),![]() (
(![]() ,0,2),D(
,0,2),D(![]() ,
,![]() ,2).所以
,2).所以![]() =(0,
=(0,![]() ,1),
,1),![]()
![]() ,
,![]() ,
,![]() ,cos(
,cos(![]() ,
,![]() )=
)=![]() .所以异面直线BE与DC所成的角为
.所以异面直线BE与DC所成的角为![]() . (2)假设点F存在,坐标为(
. (2)假设点F存在,坐标为(![]() ,0,z),则
,0,z),则![]() ,
,![]() ,
,![]() .又
.又![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() .所以
.所以![]() =-1+1+0=0,且
=-1+1+0=0,且![]() .所以
.所以![]() ,由于该方程无实数解,所以符合条件的点F不存在. (3)当F为
,由于该方程无实数解,所以符合条件的点F不存在. (3)当F为![]() 中点时,
中点时,![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() .设
.设![]() =(x,y,z)为平面
=(x,y,z)为平面![]() 的一个法向量,则
的一个法向量,则![]() ,
,![]() .所以
.所以![]() ,
,![]() ,取x=1得平面
,取x=1得平面![]() 的一个法向量
的一个法向量![]() =(1,-1,
=(1,-1,![]() ).因为
).因为![]() 在
在![]() 上的射影长为
上的射影长为![]() ,所以点C到平面
,所以点C到平面![]() 的距离为
的距离为![]()
20.由![]() ,且
,且![]() <a<1,知
<a<1,知
| x | -1<x<0 | x=0 | 0<x<a | x=a | a<x<1 |
|
| 正数 | 0 | 负数 | 0 | 正数 |
|
| 递增 | 极大值 | 递减 | 极小值 | 递增 |
由此可知,最大值仅可能在x=0及x=1处取到;最小值仅可能在x=-1及x=a处取到.因为![]() ,
,![]() ,且
,且![]() <a<1,所以
<a<1,所以![]() ,
,![]() 在x=0处取到最大值.所以
在x=0处取到最大值.所以![]() ,此时
,此时![]() .若
.若![]() 在
在![]() 处取到最小值,则
处取到最小值,则![]() ,
,![]() ,
,![]() .由于
.由于![]() 时,
时,![]()
![]() .所以
.所以![]() 符合要求.若
符合要求.若![]() 在x=a处取到最小值,则
在x=a处取到最小值,则![]() ,
,![]() ,a>1,与条件
,a>1,与条件![]() <a<1矛盾.所以所求的a、b值为
<a<1矛盾.所以所求的a、b值为![]() ,b=1
,b=1
21.(1)设A(a,0),B(0,b),C(x,y),则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .因为
.因为![]() ,
,![]() .所以
.所以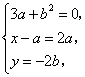 消a、b得
消a、b得![]() .所以曲线E的方程为
.所以曲线E的方程为![]() . (2)设R(x,y)为直线l上一点,则由条件知
. (2)设R(x,y)为直线l上一点,则由条件知![]() ,即
,即![]() ,
,![]() ,
,![]() .所以
.所以![]() ,且
,且![]() ,消
,消![]() 得l方程为
得l方程为![]() .由
.由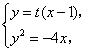 消y得
消y得![]() .设
.设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]() ,所以
,所以![]() ,且
,且![]() ,解得
,解得![]() .所以t的取值范围是
.所以t的取值范围是![]() 或
或![]()
22.(1)记圆![]() 的半径为
的半径为![]() ,由条件知,
,由条件知,![]() ,
,![]() ,
,![]() .所以
.所以![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() .所以数列
.所以数列![]() 是等差数列,公差为2. (2)由(1)知,
是等差数列,公差为2. (2)由(1)知,![]() ,
,![]() ,
,![]() .所以
.所以![]()
![]() ,因为n≥2时,
,因为n≥2时,![]() ,所以
,所以![]()
![]() ,所以
,所以
![]() .
.