高三数学学科综合能力训练(三)
【同步达纲练习】
一、选择题:(本大题共14小题;第1—10题每小题4分,第11—14题每小题5分,共 60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.sin15°cos(-375°)的值是( )
A.-![]() B.
B. ![]() C.-
C.-![]() D.
D.![]()
2.设A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则满足C![]() A∩B的集合C的个数是( )
A∩B的集合C的个数是( )
A.0 B.1 C.2 D.4
3.(文科做)已知cosx=-![]() (π<x<2π),则x等于( )
(π<x<2π),则x等于( )
A.![]() π B.
π B.![]() π C.
π C.![]() π D.
π D.![]() π
π
(理科做)已知cosx=-![]() (π<x<2π
(π<x<2π![]() ,则x等于( )
,则x等于( )
A.arccos(-![]() )
B.π+arccos(-
)
B.π+arccos(-![]() )
)
C.π+arccos![]() D.2π-arccos
D.2π-arccos![]()
4.不等式![]() >x-1的解集是( )
>x-1的解集是( )
A.(0,5)
B.[-![]() ,1]
,1]
C.[1,5]
D.[-![]() ,5)
,5)
5.已知函数y=f(x)的图像是C1,C1关于y轴对称的图像是C2,若C2关于原点对称的 图像所表示的函数是y=g(x),那么g(x)的表达式是( )
A.g(x)=f(x) B.g(x)=-f(x)
C.g(x)=f(-x) D.g(x)=-f(-x)
6.A、B分别是复数z1、z2在复平面上对应的两点,且z1·z2≠0,O是原点,若│z 1+z2│=│![]() -
-![]() │,则△AOB是( )
│,则△AOB是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
7.若a>b>0,则![]()
![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
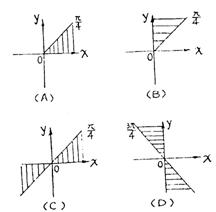
8.如果sinα+cosα=![]() (
(![]() ≤a≤1)且│sinα│≤│c osα│,那么角α的终边所在的位置(用图中阴影表示)可能是( )
≤a≤1)且│sinα│≤│c osα│,那么角α的终边所在的位置(用图中阴影表示)可能是( )
9.函数y=![]() (e为自然对数的底,e=2.71828…)的值域 是( )
(e为自然对数的底,e=2.71828…)的值域 是( )
A.(-∞,-![]() )∪(1,+∞) B.(-
)∪(1,+∞) B.(-
![]() ,1)∪(1 ,+∞)
,1)∪(1 ,+∞)
C.(- ![]() ,0)
D.(-
,0)
D.(- ![]() ,1)
,1)
10.已知数列{an}中,an=3n-30,若数列{bn}的通项bn=a1+a3+a32+…
…+![]() ,那么bn的绝对值最小项是( )
,那么bn的绝对值最小项是( )
A.b2 B.b3 C.b4 D.b5
11.已知复数ω=![]() (
(![]() < θ<
< θ<![]()
![]() ,那么argω等于( )
,那么argω等于( )
A.2θ-![]() B.2θ-
B.2θ-![]()
C.5π-2θ
D. ![]() -2θ
-2θ
12.A、B、C、D、E五人并排站成一排,如果A、B必须相邻且在C的右边,那么不同的排法有 ( )
A.60种 B.48种 C.36种 D.24种
13.用数学归纳法证明:(n+1)(n+2)……(n+n)=2n·1·3…(2n-1)(n∈N)时,从“k到k+1 ”时,左边需要相乘的代数式是( )
A.![]() B.
B. ![]()
C.2(2k+1) D.2k+1
14.(理)下列方程表示双曲线的是 ( )
A.![]() =1(-
=1(-![]() <θ<
<θ<![]() )
)
B.4ρcos2![]() =3
=3
C.|z-i|-|z+i|=2(z是复数)
D.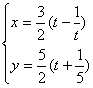
(文)已知点E(3,2),点F是抛物线x=![]() y2的焦点,点P是抛物线上一 动点,当|PE|+|PF|取最小值时,点P的坐标是( )
y2的焦点,点P是抛物线上一 动点,当|PE|+|PF|取最小值时,点P的坐标是( )
A.(1,![]() ) B.(1,1)
C.(
) B.(1,1)
C.( ![]() ,1) D.(2,2)
,1) D.(2,2)
二、填空题:(本大题共4小题;每小题4分,共16分,把答案填在题中“横线”上)
15.若正数a、b满足ab=a+b+3,则a·b的取值范围是 .
16.二项式(2x-1)12·(2x2-x)的展开式中,x2项的系数是 .
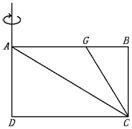
17.如图,已知点G是矩形ABCD的边AB上一点,连结AC、GC,若△AD C、△AGC和△B GC分别绕矩形AD边旋转一周所得旋转体体积相等,则AG∶GB= .
18.关于函数y=f(x)=x+![]() -1(x∈R,x≠1)有下列命题.
-1(x∈R,x≠1)有下列命题.
①y=f(x)的最小值是2;
②函数y=f(x)的图像关于(1,0)点对称;
③函数y=f(x)的图像关于x轴对称;
④函数y=f(x)在区间(-∞,1)有最大值-2.
其中,正确命题的序号是 .
三、解答题:(本大题共6小题;共74分,解答应写出文字说明、证明过程或演算步骤)
19.已知函数f(x)=5+2![]() sinxcosx-6cos2x,求:
sinxcosx-6cos2x,求:
(1)f(x)的最小正周期和f(x)的最小值;
(2)f(x)的单调递增区间.
20.(文科做)解方程:log2(2x+1+4)+log1/2(4x-4)=1.
(理科做)解不等式:log8(x-a)+log64(x+a)≥log4x(a∈R,a≠0).
21.已知复数ω=![]() (z≠±3)是纯虚数.
(z≠±3)是纯虚数.
(文科做)求实数μ=│6i-z│的最大值和最小值.
(理科做)求复数μ=6i-z的幅角主值范围.
22.红光机械厂拟更换一部发电机,已知B型发电机比A型发电机购价多1000元,但每月可节 约使用费50元(节约额于月末实现).按1%的月折现率计算(月折现率r,是指一个月后的1元, 相当于现值的![]() 元),求:
元),求:
(1)B型发电机使用2个月可节约使用费相当于现值的多少元?
(2)更换B型发电机至少使用多少月才比较合算(精确到月)?
(取lg2=0.3010,lg1.01=0.0043)
23.(文科做)已知函数y=![]() ,(x>1,ax+1≠0,且a≤0)当y<0时,求 a的取值范围.
,(x>1,ax+1≠0,且a≤0)当y<0时,求 a的取值范围.
(理科做)已知函数f(x)=-x2+(m+n)x+2m-n和函数g(x)=![]() ,对于任意 实数x(x≠-
,对于任意 实数x(x≠-![]() ),总有g[g(x)]=x恒成立,当x∈[-1,2]时,f(x) 有最大值
),总有g[g(x)]=x恒成立,当x∈[-1,2]时,f(x) 有最大值![]() ,求m、n的值.
,求m、n的值.
24.已知曲线C1的方程是2x2-y2=2m2(m>0),抛物线C2的顶点在坐标原点,抛物 线的焦点是双曲线C1的左焦点F.
(1)求证:双曲线C1与抛物线C2有且只有两个公共点;
(2)是否存在过F的抛物线C2的弦PQ,使△POQ的面积为6cm2,若存在,求出PQ所在直线的倾斜角;若不存在,请说明理由.
参考答案
【同步达纲练习】
一、选择题:
1.B 2.C 3.文A 理C 4.D 5.B 6.B 7.A 8.A 9.D 10.C 11.A 12.D 13.C 14. 文D 理D.
二、填空题
15.[9,+∞)
16.26 17.![]() 18.②④.
18.②④.
三、解答题
19.解:(1)∵f(x)=![]() sin2x-6·
sin2x-6·![]() +5
+5
=![]() sin2x-3cos2x+2
sin2x-3cos2x+2
=2![]() sin(2x-
sin(2x-![]() )+2.
)+2.
∴T=![]() =
=![]() =π.
=π.
∴当sin(2x-![]() )=-1时,有最小值2-2
)=-1时,有最小值2-2![]() .
.
(2)设2kπ-![]() ≤2x-
≤2x-![]() ≤2πk+
≤2πk+![]() ,
,
2kπ-![]() ≤2x≤2kπ+
≤2x≤2kπ+![]() .
.
∴kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() (k∈Z).
(k∈Z).
∴f(x)的递增区间为[kπ-![]() ,kπ+
,kπ+![]() π].
π].
20.(文科做)
解:原式变为:log2(2x+1+4)-log2(4x-4)=log22,
∴![]() =2.
=2.
令2x=y,原方程变形为y2-y-6=0,∴y1=3或y2=-2(舍去).
当y1=3时,2x=3,∴x=log23.
检验知x=log23是原方程的根.
(理科做)
解:由log8(x-a)+log64(x+a)≥log4x(a∈R,且a≠0),变形为![]() log2(x-a)+
log2(x-a)+![]() log2(x+a)≥
log2(x+a)≥![]() log2x.
log2x.
∴原不等式等价于不等式组:
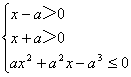
1°当a>0时,不等式组等价于
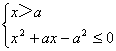
即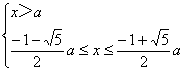 (无解).
(无解).
2°当a<0时,不等式组等价于
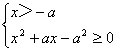 即
即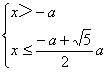 (无解).
(无解).
或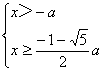 解得x≥
解得x≥![]() a.
a.
综上所知,当a<0时,x≥![]() a,
a,
当a>0时,无解.
21.解1:令z=x+yi(x,y∈R)
∴ω=![]()
=![]()
=![]()
∵ω是纯虚数,∴x2+y2=9,∴│z│=3.
解2:∵ω是纯虚数,∴ω+![]() =0,
=0,
即![]() =0
=0![]() z
z![]() =9,∴│z│=3.
=9,∴│z│=3.
(文科做)由题意知│6i│-│z│≤μ≤│6i│+│z│,
即6-3≤μ≤6+3,∴3≤μ≤9.
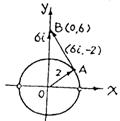
(理科做)复数μ=6i-z,可表示为在复平面上,以(0,0)为圆心,3为半径的圆周上动点A到 定点B(0,6)的有向线段![]() (如图).
(如图).
1°当![]() 与圆在第Ⅰ像限相切时,有最大幅角主值为
与圆在第Ⅰ像限相切时,有最大幅角主值为![]() + ∠OBA=
+ ∠OBA=![]() +
+![]() =
=![]() π.
π.
2°当![]() 与圆在第Ⅱ像限相切时,有最小幅角主值为
与圆在第Ⅱ像限相切时,有最小幅角主值为![]() -
-![]() =
=![]() ,∴
,∴![]() ≤argμ≤
≤argμ≤![]() π.
π.
22.解:(1)使用两个月节约费用100元,相当于现值的50×![]() +50(
+50(![]() )2=50[
)2=50[![]() +(
+(![]() )2]≈98 .5(元).
)2]≈98 .5(元).
(2)B型发电机使用3个月节约费用相当于现值的50×[![]() +(
+(![]() )2+(
)2+(![]() )3],使用n个月节约费用相当于现值的50[
)3],使用n个月节约费用相当于现值的50[![]() +(
+(![]() )2+…+(
)2+…+(![]() )n].
)n].
设更换B型发电机至少使用n个月才比较合算,则50[![]() +(
+(![]() )2+……+(
)2+……+(![]() )n]≥1000,即50·
)n]≥1000,即50·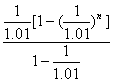 ≥1000.
≥1000.
∴1.01n≥![]() ,nlg1.01≥lg
,nlg1.01≥lg![]()
![]() n≥
n≥![]() ≈
≈![]()
![]() n≈23.
n≈23.
答:(略).
23.(文科做)解:![]() <0.
<0.
1°当a=0时,y=-1<0,对任意x>1均满足不等式.
2°当a<0时,原不等式等价于
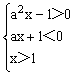 (Ⅰ) 或
(Ⅰ) 或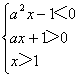 (Ⅱ)
(Ⅱ)
由(Ⅰ)解得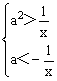 又x >1,
又x >1,
∴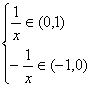
∴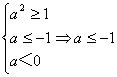
由(Ⅱ)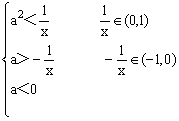
∴a2<0(无解).
综合知a的取值范围为a=0,或a≤-1.
(理科做)解:
∵g[g(x)]=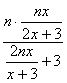 =
=![]() =x,
=x,
即(2n+6)x2+(9-n2)x=0.
∵对任意的x上式均成立.
∴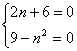 解得n=-3.
解得n=-3.
∴f(x)=-x2+(m-3)x+2m+3.
其对称轴为x=![]() .
.
1°当-1<![]() <2,即1<m<7时,
<2,即1<m<7时,
f(x)max=f(![]() )=
)=![]()
∴m=-4(舍去)或m=2.
2°当![]() ≤-1,即m≤1时,
≤-1,即m≤1时,
fmax(-1)=m+5=![]() ,
,
∴m=![]() 与m≤1矛盾,无解.
与m≤1矛盾,无解.
3°当![]() ≥2,即m≥7时,
≥2,即m≥7时,
fmax(2)=-4+2(m-3)+2m+3=4m-7=![]() .
.
∴m=![]() 与m≥7矛盾,无解.
与m≥7矛盾,无解.
综上知,符合要求的值为
n=-3,m=2.
24.(1)由2x2-y2=2m2,有![]() -
-![]() =1
①
=1
①
双曲线的左焦点为F(-![]() m,0).由题意,可设抛物线方程y2=-2px,则
m,0).由题意,可设抛物线方程y2=-2px,则![]() m,即p=-2
m,即p=-2![]() .
.
抛物线方程为 y2=-4![]() mx
②
mx
②
把②代入①,整理得x2+2![]() mx-m2=0
③
mx-m2=0
③
方程③的判别式
△=(2![]() m)2-4(-m2)=16m2>0,
m)2-4(-m2)=16m2>0,
x1x2=-m2<0,x1、x2异号,不妨设x1>0,x2<0,对x1>0,它不适合方程②,应舍 去,故只有x2<0满足方程②,此方程②有且只有两组实数解.
C1和C2有且只有两个公共点.
(2)设过F的直线的倾斜角为α.
当α≠![]() ,过F的直线为y=k(x+
,过F的直线为y=k(x+![]() m),
m),
x=![]() -
-![]() m
④
m
④
把④代入②,得y2=-4![]() m(
m(![]() -
-![]() m)
m)
即y2+![]() y-12m2=0
y-12m2=0
|PQ|=![]() |y1-y2|=
|y1-y2|=![]() ·
·![]()
=![]() ·
·![]()
原点O到PQ的距离为d=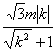 ,
,
![]() =
=![]() |PQ|·d=
|PQ|·d=![]() ·
·![]() ·
·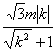
=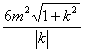
令 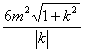 =6m2,则
=6m2,则![]() =|k| 故k不存在.
=|k| 故k不存在.
当a=![]() 时,过F的直线方程为x=-
时,过F的直线方程为x=-![]() m
⑤
m
⑤
把⑤代入②,得
y2=-4![]() m(-
m(-![]() m)=12m2,
m)=12m2,
y=±2![]() m 所以|PQ|=4
m 所以|PQ|=4![]() m
m
从而S△POQ=![]() |PQ|(
|PQ|(![]() m)=
m)=![]() ·4
·4![]() m·
m·![]() m=6m2
m=6m2
a=![]() 符合题设要求.
符合题设要求.
综上知,存在过F的抛物线C2的弦PQ,使△POQ的面积为6m2,这样的直线的倾斜角为![]() .
.