高三数学原创题

高三数学原创题

原创题1

[题目]质地均匀的正方体木块的棱长为n,n为正整数且n≥2.在其表面涂上与材质颜色不同的蓝色后将木块分割成棱长为1的小正方体木块,假设从中任意取一块得到表面有蓝色的木块的概率为P,请研究P能否大于或小于.

 [解答]:

当n=2时, P=1;

当n≥3时,有P=,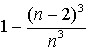

P-=.

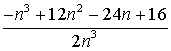记y=g(x)= , x>2.

g′(x)= ,

可知在(2,+∞)上y= g(x)只有一个极大值点x=,

所以函数y= g(x)在(2, )上是增函数;在(,+∞)上是减函数.

又验证g(3)>0, g(9) >0, g(10)<0,

于是我们得到结论:当正整数2≤n≤9时, P>;当正整数n≥10时, P<.

[说明] 本题考查概率、导数、不等式的有关知识.由江苏海安高级中学游余祥命题,难度系数预计0.65.

原创题2

[题目]设定义在[x₁,x₂]上的函数y=f(x)的图象为C,C的端点为点A、B,M是C上的任意一点,向量=( x₁,y₁), =( x₂,y₂), =(x,y),若x= x₁+(1-) x₂,记向量=+(1-).现在定义”函数y=f(x)在[x₁, x₂]上可在标准k下线性近似”是指≤k恒成立,其中k是一个人为确定的正数.

(1)证明: 0≤≤1;

(2)请你给出一个标准k的范围,使得[0,1]上的函数y=x²与y=x³中有且只有一个可在标准k下线性近似.

 [解答]:

(1)由题意, x₁≤x≤x₂即x₁≤ x₁+(1-) x₂≤x₂,

∴x₁- x₂≤(x₁- x₂) ≤0,

∵x₁- x₂<0,

∴0≤≤1.

(2)由=+(1-)得到=,

所以B、N、A三点在一条直线上,

又由(1)的结论, N在线段AB上且与点M的横坐标相同.

对于 [0,1]上的函数y=x²,A(0,0),B(1,1),

则有= x- x²=,故[0, ];

对于[0,1]上的函数y=x³, 则有= x- x³= g(x),

在(0,1)上, g′(x)= 1-3 x²,

可知在(0,1)上y= g(x)只有一个极大值点x=,

所以函数y= g(x)在(0, )上是增函数;在(,1)上是减函数,又g()=

故[0, ].

经过比较, <,所以取k[,),则有函数y=x²在[0,1]上可在标准k下线性近似,函数y=x³在[0,1]上不可在标准k下线性近似.

[说明] 本题考查向量、函数、导数、不等式的有关知识.由江苏海安高级中学游余祥命题,难度系数预计0.60.

原创题3

[题目]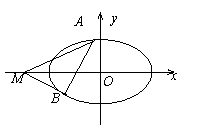如图1，过椭圆的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在轴上，且使得MF为的一条内角平分线，则称点M为该椭圆的“左特征点”.

（1）求椭圆的“左特征点”M的坐标；

图1

（2）试根据（1）中的结论猜测：

椭圆的“左特征点”M是一个怎样的点？并证明你的结论.

解析： （1）设为椭圆的左特征点，椭圆的左焦点为，可设直线的方程为.并将它代入得：，即.

设，则，

∵被轴平分，∴.

即.

即.

∴.

于是.

∵，即.

（2）对于椭圆.于是猜想：椭圆的“左特征点”是椭圆的左准线与轴的交点.

证明：设椭圆的左准线与轴相交于M点，过A，B分别作的垂线，垂足分别为C，D.

据椭圆第二定义：

∵

于是即.

∴，又均为锐角，

∴，∴.

∴的平分线.故M为椭圆的“左特征点”.

原创题4

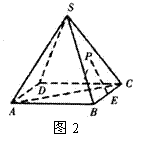
[题目]如图2，在正四棱锥S－ABCD

中，E是BC的中点，P点在侧面内

及其边界上运动，并且总是保持PEAC.

（1）指出动点P的轨迹（即说明动点P在满足给定的条件下运动时所形成的图形），证明你的结论；

（2）以轨迹上的动点P为顶点的三棱锥P－CDE的最大体积是正四棱锥S－ABCD体积的几分之几？

（3）设动点P在G点的位置时三棱锥P－CDE的体积取最大值V₁，二面角G－DE－C的大小为，二面角G－CE－D的大小为，求的值.

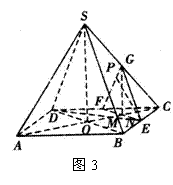（4）若将“E是BC的中点”改为“E是BC上异于B、C的一定点”，其它条件不变，请指出点P的轨迹，证明你的结论.

解析：（1）如图3，分别取CD、SC

的中点F、G，连结EF、EG、FG、BD.设　　　　　　　　　　　　

AC与BD的交点为O，连结SO，则动点

P的轨迹是的中位线FG.

由正四棱锥可得.又

平面EFG，平面EFG，.

（2）由于是定值，所以当P到平面CDE的距离最大时，最大，易知当P与G重合时，P到平面CDE的距离最大，故.又，G到平面ABCD的距离是点S到平面ABCD的距离的，

.

（3）令，EF与AC交于N点，连结GN，则GN平面ABCD.

因此二面角G－DE－C和二面角G－CE－D的平面角的正切值的比就等于N到DE和CE的距离的倒数比.

N是OC的中点，N到BC的距离为.

连结DE交OC于M，则M是的重心，.

又，

在中，容易求得N到DE的距离为.

故.

（4）动点P在侧面SCD内部及其边界上运动，且总保持，那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内，而由正四棱锥的性质可知，平面SBD，因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E//SB，E//BD，分别交SC于，交CD于，则平面E//平面SBD，从而平面E，故点P的轨迹是线段.