高三数学章节测试（选修Ⅱ）
本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 共150分.
考试时间120分钟.
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．关于函数y=f(x)，下列说法中，正确的是（ ）
A．若f(x)在x＝x0处连续，则
B．若f(x)在x＝x0处连续，则f(x)在x＝x0处可导
C．若f(x)在x＝x0处有极限，则f(x)在x＝x0处可导
D．若f(x)在x＝x0处的导数等于0，则f(x)在x＝x0处有极值
2．复平面内，复数z=(x2-x-30)+(x2+x-12)i (x∈R)对应的点位于第二象限，则x的取值集合（ ）
A．(-5，+6) B．(-4，3) C．Φ D．(-5，-4)∪(3，6)
3．要完成下列2项调查：①从某社区125户高收入家庭，280户中等收入家庭，95户低收入家庭中选出100户调查社会购买力的某项指标；②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况。应采用的抽样方法是（ ）
A．①用随机抽样法 ②用系统抽样法
B．①用分层抽样法 ②用随机抽样法
C．①用系统抽样法 ②用分层抽样法
D．①、②都用分层抽样法
4．用数学归纳法证明
时，由
的假设到证明
时，等式左边应添加的式子是（ ）
A．
B．
C．
D．
5．已知函数y=xcosx,则y′x=0等于( )
A.1 B.0 C.-1 D.2
6．x=1是函数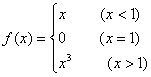
的（ ）
A．连续点 B．无定义点 C．不连续点 D．极限不存在的点
7、点P是曲线
上任意一点，则点P到直线
的最小距离为 （ ）
A.1 B. 
C.
D.
8．函数
处的切线方程是（ ）
A．
B．
C．
D．
9．已知a、b是不相等的正数，若
，则b的取值范围是（ ）
A．0＜b≤2 B．0＜b＜2 C．b≥2 D．b＞2
10．某校有教职员工150人，为了丰富教工的课余生活，每天定时开放健身房和娱乐室。据调查统计，每次去健身房的人有10%下次去娱乐室，而在娱乐室的人有20%下次去健身房。随着时间的推移，去健身房的人数能稳定在（ ）
A．50人 B．120人 C．100人 D．80人
11．已知函数
有极大值和极小值，则a的取值范围是（ ）
A．
B．
C．
D．
|
A．
B．
C．
D．
数学章节测试（选修Ⅱ）答题卷
班级__________ 姓名__________ 分数__________
选择题答题框
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分
13．10．一个容量为20的样本数据，分组后，组距与频数如下：
10，20
，2；（20，30，3；（30，40，4；（40，50 ，5；（50，60 ，4；（60，70 ，2；则样本在（50，+∞）上的频率为__________
14．在直线轨迹上运行的一列火车，从刹车到停车这段时间内，测得刹车后t秒内列车前进的距离s＝27t－0.45t2（单位是米），这列火车在刹车 秒钟后停车。
15．等比数列{an}满足
的取值范围是
16．已知：
则
________
三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.
17．（本小题满分12分）求函数
在区间
上的最大值和最小值.
]
18．（本小题满分12分）已知等比数列
，
，
，且
，求
19．（本小题满分12分）在一次环保知识竞赛中，有6道选择题和2道判断题放在一起供抽取，每支代表队要抽3次，每次只抽一道题回答.
（1）不放回的抽取试题，求只在第三次抽到判断题的概率；
（2）有放回的抽取试题，求在三次抽取中抽到判断题的个数
的概率分布及的期望.
20．（本小题满分12分）已知数列满足
,且前
项和
.
（1）求
；
（2）猜测
的表达式，并用数学归纳法证明。
21．（本小题满分12分）证明：当
时，
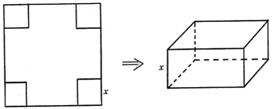
22．（本小题满分14分）从边长为2a的正方形铁片的四个角各截去一个边为x的正方形，再将四边向上折起，做成一个无盖的长方形铁盒，要求长方体的高度与底面边的比值不超过常数t（t>0）。试求容积V与x的函数关系,当x取何值时，容积V有最大值.
