高三数学周考卷（8）
第Ⅰ卷(选择题 50分)
一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1．已知集合
，则实数a的取值范围是
（A）[1，2] （B）（－1，2） （C）[－1，2] （D）（－2，1）
⒉ 设0<a<1，实数x,y满足x+
=0，则y关于x的函数的图象大致形状是
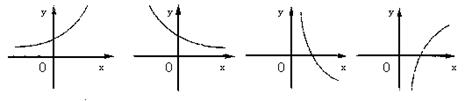
A B C D
3． 若向量
=(3，－1)，n=(2，1)，且n
=7，那么n
=
A．－2 B．2 C．－2或2 D．0
4．下列判断错误的是 A．命题“若q则p”与命题“若
”互为逆否命题
B．“am2<bm2”是“a<b”的充要条件
C．“矩形的两条对角线相等”的否命题为假
D．命题“
”为真（其中
为空集）
5. 若函数
的值域是
，则其反函数
的值域是
A． B．
C．
D．
6．函数
与函数
在[0，
]上单调性相同,则的一个值为
A．
B．
C．
D．
7． 在2与7之间插入n个数, 使这个以2为首项的数列成等差数列, 并且S16＝56则n＝
A. 26 B. 25 C. 24 D. 23
8. 两位同学一起去一家单位应聘, 面试前单位负责人对他们说:“我们要从面试的人中招聘3人,你们俩同时被招聘进来的概率是
”.根据这位负责人的话可以推断出参加面试的人数为
A. 21 B. 35 C. 42 D. 70
9. 已知∠Ｃ＝９０°，AC=BC，M、N分别为BC和AB的中点，沿直线MN将△BMN折起，使二面角Ｂ′－MN－Ｂ为60°，则斜线Ｂ′Ａ与平面ABC所成角的正切值为
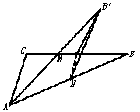
A.
B.
C. 
D.
10．将直线x+y=1绕点（1，0）顺时针旋转90º，再向上平移1个单位后，与圆
相切，则半径
的值是
A．1 B．
C．
D．
第Ⅱ卷（非选择题 100 分）
二、填空题：本大题共5小题，每小题4分，共20分。将答案填在横线上。
11 
展开式的第三项为
12．已知双曲线
的一条准线是y=1，则实数k的值是______
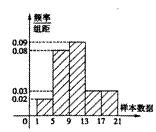13.右图是一个容量为200的样本的频率分布直方图，请根据图形中
的数据填空：
（1）样本数据落在范围
的频率为
；
（2）样本数据落在范围
的频数为
；
14．设x，y满足约束条件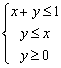
，则z＝3x＋y的最大值是
15. 球面上有A、B、C三点，AB=AC=2，BC=2
，球心到平面ABC的距离为1，则球的
表面积为
三、解答题：本大题共6小题,共80分,解答应写出文说明、证明过程或演算步骤
16．（本小题满分12分）
已知向量
＝（m－sinx，－1），
＝（1，cosx），且
＝1，m、x∈R.
（Ⅰ）把m表示为x的函数f(x)，并求该函数的最小值；
（Ⅱ）把函数的图象按向量＝（
，1）平移得到
，求的函数式.
17.(本小题满分12分)
设
．
(Ⅰ)求函数f (x)的单调区间；
(Ⅱ）当x∈[
，2]时，
恒成立，求实数m的取值范围．
18. (本小题满分14分)
从汽车东站驾车至汽车西站的途中要经过8个交通岗，假设某辆汽车在各交通岗遇到红灯的事件是独立的，并且概率都是
.
（Ⅰ）求这辆汽车首次遇到红灯前，已经过了两个交通岗的概率;
（Ⅱ）求这辆汽车在途中恰好遇到4次红灯的概率．
19．（本小题满分14分）
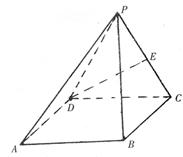
如图，四棱锥P—ABCD中，底面四边形ABCD是正方形，侧面PDC是边长为a的正
|
（I）求异面直线PA与DE所成的角；
（II）求点D到面PAB的距离.
20．（本小题满分14分）
已知数列
，设Sn是数列的前n项和，并且满足a1=1，对任意正整数n，
（Ⅰ）令
证明
是等比数列，并求的通项公式；
（Ⅱ）令
的前n项和，求
21．（本小题满分14分）
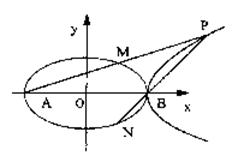
已知椭圆
的一条准线方程是
其左、右顶点分别是A、B；双曲线
的一条渐近线方程为3x－5y=0.
（Ⅰ）求椭圆C1的方程及双曲线C2的离心率；
（Ⅱ）在第一象限内取双曲线C2上一点P，连结AP交椭圆C1于点M，连结PB并延长交椭圆C1于点N，若
. 求证：
|
参 考 答 案
一. BABBC DCABB
二．11．
12. 
13.
0.32 72 14.3 15.
三． 16（Ⅰ）
，最小值为
……………………..7分
（Ⅱ）
………………………………12分
| x |
| 1 | |||
| f /(x) | ＋ | 0 | － | 0 | ＋ |
| f (x) | ↗ | ↘ | ↗ |
| |
……………………………… 2分令
得x = 1或
列表如下
4分
∴函数单调递增区间为(－∞，
]、[1，＋∞)，单调递减区间为[
，1]．…...6分
(Ⅱ)解：由(1)得，在区间[－1，1]上，是最大值点，其最大值为
．
………………………… 8分
当x∈[1，2]时，函数单调递增，∴其最大值为f (2) = 7
………………… 10分
∴当x∈[，2]时，函数f (x)的最大值为7．
故恒成立时实数m的取值范围为(7，＋∞)．…………………………..12分
18．（I）∵ 这辆汽车在第一、二个交通岗均未遇到红灯，而第三个交通岗遇到红灯
∴ 概率
= (1 –
)(1 –) = 
; ………………………7分
（II） 概率 = 
´()4´ (1–)4 = 
. ……………………14分
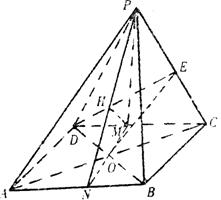
19． （I）解法一：连结AC，BD交于点O，连结EO.
∵四边形ABCD为正方形，∴AO=CO，又∵PE=EC，∴PA∥EO，
∴∠DEO为异面直线PA与DE所成的角……………………3分
∵面PCD⊥面ABCD，AD⊥CD，∴AD⊥面PCD，∴AD⊥PD.
在Rt△PAD中，PD=AD=a，则
，
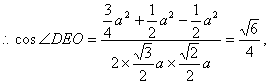
∴异面直线PA与DE的夹角为
……………………7分
（Ⅱ）取DC的中点M，AB的中点N，连PM、MN、PN.
|
∴D到面PAB的距离等于点M到
面PAB的距离.……7分
过M作MH⊥PN于H，
∵面PDC⊥面ABCD，PM⊥DC，
∴PM⊥面ABCD，∴PM⊥AB，
又∵AB⊥MN，PM∩MN=M，
∴AB⊥面PMN. ∴面PAB⊥面PMN，
∴MH⊥面PAB，
则MH就是点D到面PAB的距离.……10分
在
|
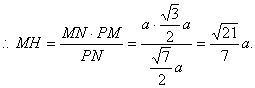………………14分
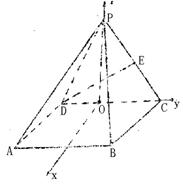
解法二：如图取DC的中点O，连PO，
∵△PDC为正三角形，∴PO⊥DC.
又∵面PDC⊥面ABCD，∴PO⊥面ABCD.
如图建立空间直角坐标系
则
.………………………………3分
（I）E为PC中点，
，
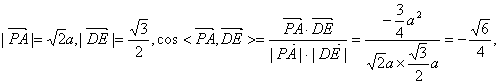
∴异面直线PA与DE所成的角为……………………7分
（Ⅱ）可求
，
设面PAB的一个法向量为
，
① 
. ②
由②得y=0，代入①得
令
…………………………10分
则D到面PAB的距离d等于
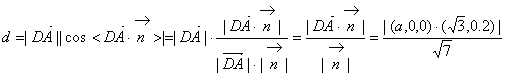
即点D到面PAB的距离等于
……………………………14分
20.（I）证明：
① （2分）
由题知
又由①
是等比数列，公比q=2，…………. 5分
又
…………….8分
（Ⅱ）解：
………….12分
…...14分
21．（I）由已知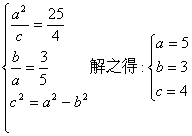
………………3分
∴椭圆的方程为
，双曲线的方程
.
又
∴双曲线的离心率
…………………………6分
（Ⅱ）由（Ⅰ）A（－5，0），B（5，0） 设M
得m为AP的中点
∴P点坐标为
将m、p坐标代入c1、c2方程得
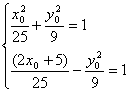
消去y0得
解之得
由此可得P（10，
………………10分
当P为（10， 时 PB：
即
代入
MN⊥x轴 即
…………14分