高三数学周练试卷(1)
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)，全卷满分150分，考试时间120分钟.
第Ⅰ卷（选择题 共60分）
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．设P，Q为两个非空实数集合，定义集合P+Q={a+ba∈P，b∈Q}，若P={0，2，5}，Q={1，2，6}，则P+Q中元素的个数是 （ ）
A.9 B.8 C.7 D.6
2．已知
，则
的值是 （ ）
A．
B． 
C．
D．
3．函数
的反函数是
（ ）
A．
B．
C．
D．
4．“ 2x – 1 < 3”是“
< 0”的
( )
(A) 必要不充分条件 (B) 充分不必要条件
(C) 充要条件 (D) 既不充分也不必要条件
5．等差数列
前四项和为40, 末四项和为72, 所有项和为140, 则该数列共有 （ ）
A．9项 B．12项 C．10项 D．13项
6.要得到函数y=3f(2x+
)的图象，只须将函数y=3f(2x)的图象 ( )
A.向左平移个单位 B.向右平移
个单位
C.向左平移个单位 D.向左平移
个单位
7.如果直线
与直线
关于直线
对称, 那么
( )
A.
B.
C. 
D. 
8．已知函数
在区间(
，1)上有最小值，则函数
在区间(1，
上一定
( )
A．有最小值 B．有最大值 C．是减函数 D．是增函数
9．已知A、B为锐角三角形的两个内角，设m=cosB，n=sinA，则下列各式中正确的是（ ）
A.m<
<n
B.m<n<
C.n<m< D.n<<m
10．给定正数
,其中
,若
成等比数列,
成等差数列,则一元二次方程 
（ ）
A．无实数根 B．有两个相等的实数根
C．有两个同号的相异的实数根 D．有两个异号的相异的实数根
11．函数
的图象的一条对称轴方程为
，则直线
的倾斜角
( )
A．45° B．135° C．60° D．120°
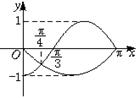
12.已知函数y=f（x）是偶函数，y=g（x）是奇函数，它们的定义域为［－π，π］，且它们在x∈［0，π］上的图象如下图所示，则不等式
＞0的解集为 ( )
A.（－
，0）∪（，π）
B.（－π，－）∪（，π）
C.（－
，0）∪（，π）
D.（－π，－）∪（0，）
第Ⅱ卷（非选择题 共90分）
二．填空题：本大题共4小题，每小题4分，共16分．把答案填写在相应的位置上．
13．设向量 
绕点 
逆时针旋转 
得向量 
, 且 
, 则
向量 
.
14.将直线y＝－
x+2绕点(2,0)按顺时针方向旋转60°所得的直线
在y轴上的截距是_________
15．已知e1、e2是两个不共线的向量，a = k2e1
+ (
k)e2和b = 2e1 + 3e2是两个共线向量，则实数k = ．
16．给出四个命题：①存在一个△ABC，使得sinA+cosA=－1;②△ABC中,A＞B的充要条件为sinA＞sinB;③直线x=
是函数y=sin(2x+
)图象的一条对称轴；④△ABC中，若sin2A=sin2B,则△ABC一定是等腰三角形.
，则其中正确命题的序号为______________
三．解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．
17．(本小题满分12分)
已知函数f(x)＝
⑴当a＝1时，求f(x)的单调递增区间；
⑵当a<0时，且x∈[0，π]时，f(x)的值域是[3，4]，求a、b的值．
18．（本题满分12分）
已知实数
满足不等式
，试判断方程
有无实根，并给出证明．
19．(本小题满分12分)
已知数列{an}的前n项和为Sn，且an＋Sn＝1(n∈N＊)。
⑴求数列{an}的通项公式；
⑵若数列{bn}满足b1＝1，且bn+1＝bn＋an(n≥1)，求数列{bn}的通项公式．
20．(本小题满分12分)
已知
，
为常数且
，求使
成立的
的范围．
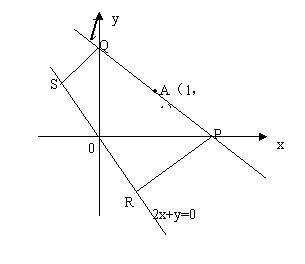
21. (本小题满分12分)
过点
作直线与
、
轴的正方向分别交于
、
两点, 又分别过点、作直线
的垂线, 垂足依次为 
、
.求四边形
面积的最小值.
22.（本小题满分14分，第一小问满分4分，第二、三小问满分各5分）
设关于x的一元二次方程
有两个实根x1，x2.
（1）求
的值；
（2）求证：
；
（3）如果
试求
的最大值.