高三下学期数学模拟试题(二)
一、选择题:本小题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)sin15°cos165°的值是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)已知三条直线m、n、l,三个平面![]() ,下面四个命题中,正确的是( ).
,下面四个命题中,正确的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(3)已知![]() (-2,5),
(-2,5),![]() ,且
,且![]() 与
与![]() 方向相反,那么
方向相反,那么![]() =( ).
=( ).
A.(4,-10) B.![]() C.(-4,10) D.
C.(-4,10) D.![]() ,
,![]()
(4)函数![]() 的单调递增区间是( ).
的单调递增区间是( ).
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
(5)一直线![]() 与圆
与圆![]() 交于A、B两点,则线段AB的垂直平分线的方程是( ).
交于A、B两点,则线段AB的垂直平分线的方程是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(6)已知在一个球的球心两侧有相距为7的两个平行截面,截面面积分别为9p 和16 p .那么这个球的表面积为( ).
A.![]() B.100 p C.64 p
D.36 p
B.100 p C.64 p
D.36 p
(7)口袋里有5个黑球和3个白球,每次任意取出一个球,若取出黑球,则放回袋中重新取球;若取出白球,则停止取球,那么正好在第4次取球后停止取球的概率是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(8)若一个等差数列前3项和为34,最后3项的和为146,且所有项的和为390,则这个数列共有( ).
A.13项 B.12项 C.11项 D.10项
(9)已知函数![]() 在
在![]() 处有极值,则
处有极值,则![]() 的递减区间是( ).
的递减区间是( ).
A.![]() ,
,![]() ,
,![]() B.(1,5)
B.(1,5)
C.(2,3)
D.![]() ,
,![]() ,
,![]()
(10)F1、F2是椭圆的左、右两焦点,以F2为圆心,OF2为半径的圆与椭圆交于点M,O是原点,如果F1M正好是这个圆的一条切线,则这个椭圆的离心率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(11)![]() ( ).
( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(12)已知![]() 是定义在R上的奇函数,
是定义在R上的奇函数,![]() ,若当
,若当![]() 时,
时,![]() ,则
,则![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题4小题,每小题4分,共16分,把答案填在题中横线上.
(13)![]() 的值为________.
的值为________.
(14)正方形ABCD、ABEF有公共边AB,它们所成二面角为60°,那么异面直线AC、BF所成角的余弦值为________.
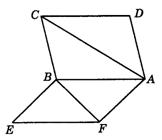
综8
(15)双曲线![]() 的离心率小于2,那么实数k的取值范围是________.
的离心率小于2,那么实数k的取值范围是________.
(16)![]() =________.
=________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分12分)
解关于x的不等式![]() .
.
(18)(本小题满分12分)
ABCD是四边形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ∥
∥![]() ,求x、y间的关系;
,求x、y间的关系;
(Ⅱ)若![]() ∥
∥![]() ,
,![]() ⊥
⊥![]() ,求x、y的值.
,求x、y的值.
(19)(本小题满分12分)
如图综9,四面体ABCD中,AB、BC、BD两两垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成角的正弦为![]() .
.
(Ⅰ)求二面角D-AC-B的平面角的正切值;
(Ⅱ)求点B到平面ACD的距离.
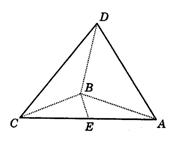
综9
(20)(本小题满分12分)
南方某林场有荒山3250亩,从1996年1月开始在该荒山上植树造林,且每年种树全部成活.第一年植树100亩,此后每年都比上一年多植树50亩.
(Ⅰ)问至少需多少年才能把此荒山全部绿化?
(Ⅱ)如果新种树苗每亩木材量为2立方米,树木每年的自然增材率为10%,那么到此荒山全部绿化后的那一年底,这林场树木的木材量总共有多少立方米?(可用1.111≈2.7)
(21)(本小题满分12分)
(Ⅰ)a取什么值时,直线![]() 是曲线
是曲线![]() 的切线?
的切线?
(Ⅱ)a取什么范围内值时,函数![]() 在区间(-1,1)内是减函数?
在区间(-1,1)内是减函数?
(22)(本小题满分14分)
已知抛物线![]() 的准线与x轴交于M点,过点M作直线与这个抛物线交于两个不同的点A、B,线段AB的垂直平分线与x轴交于E(x0,0).
的准线与x轴交于M点,过点M作直线与这个抛物线交于两个不同的点A、B,线段AB的垂直平分线与x轴交于E(x0,0).
(Ⅰ)求x0的取值范围.
(Ⅱ)△![]() 能否是等边三角形?若能,求x0的的值;若不能,说明理由.
能否是等边三角形?若能,求x0的的值;若不能,说明理由.
参考答案
一、选择题:
(1)C (2)D (3)A (4)B (5)A (6)B
(7)C (8)A (9)C (10)D (11)D (12)B
提示:
(3)设![]() ,则
,则![]() ,
,![]() .于是有
.于是有![]() .
.
(4)函数![]() ,
,![]() 复合而成,又函数
复合而成,又函数![]() 在
在![]() 上是增函数,只要求
上是增函数,只要求![]() 的递增区间.
的递增区间.
(5)所求直线过已知圆圆心,且与已知直线垂直.
(6)设球半径为R,则![]() .解得
.解得![]() .
.
(7)从口袋里任取一球是黑球的概率是![]() ,是白球的概率是
,是白球的概率是![]() .这四次取球是前三次都为黑球,第4次为白球.
.这四次取球是前三次都为黑球,第4次为白球.
(8)设等差数列公差为d,共n项,则有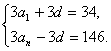 故有
故有![]() .
.![]() .
.
(9)![]() ,由
,由![]() 可得
可得![]() .
.
∴ ![]() ,由
,由![]() 解得
解得![]() .
.
(10)由![]() 可得
可得![]() .
.
(11)只要验![]() .
.
(12)由于![]() 是奇函数,故
是奇函数,故![]() ,又
,又![]() ,
,![]() ,即
,即![]() ,
,
∴ ![]() .
.
二、填空题:
(13)![]() (14)
(14)
![]() (15)
(15)
![]() (16)97
(16)97
提示:
(13)![]() .
.
(14)取BC中点G,AB中点H,AF中点P,BE中点Q,设AB=2,则![]() ,
,![]() ,
,![]() .
.
(15)双曲线方程变为![]() .于是
.于是![]() .
.
(16)![]() .
.
三、解答题:
(17)![]() .
.
当![]() 时,不等式为
时,不等式为![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() .
.
于是可得当![]() 时,原不等式解为
时,原不等式解为![]() ;
;
当![]() 时,原不等式解为
时,原不等式解为![]() ;
;
当![]() 时,原不等式解为
时,原不等式解为![]() 或
或![]() .
.
(18)(Ⅰ)![]() (6,1)+(x,y)+(-2,-3)=(x+4,y-2).
(6,1)+(x,y)+(-2,-3)=(x+4,y-2).
由![]() ,故
,故![]() ,即
,即![]() .
①
.
①
(Ⅱ)![]() (6,1)+(x,y)=(x+6,y+1),
(6,1)+(x,y)=(x+6,y+1),![]() (x,y)+(-2,-3)=(x-2,y-3).
(x,y)+(-2,-3)=(x-2,y-3).
由![]() ,故
,故![]() .
②
.
②
由①,②解得![]()
![]()
(19)(Ⅰ)取CD中点F,连结BF、EF.∴ EF∥AD,∠BEF为AD,BE所成角,![]() ,
,![]() .
.
∵ AB=BC,设BD=x,则![]() .连结DE,故
.连结DE,故![]() ,
,![]() ,
,
∴ ∠BED为二面角D-AC-B的平面角.
可以求得![]() ,
,![]() ,
,![]() .由余弦定理可求得
.由余弦定理可求得![]() .
.
在Rt△![]() 中,
中,![]() .
.
(Ⅱ)过B作![]() 于H.∵平面
于H.∵平面![]() 平面ACD,∴
平面ACD,∴![]() 平面ACD,即BH为B到平面ACD的距离,由
平面ACD,即BH为B到平面ACD的距离,由![]() 可求得
可求得![]() .
.
(20)(Ⅰ)设至少要n年才能把此荒山全部绿化,第一年,第二年,第三年,…所种树的亩数成等差数列,首项为100,公差为50,于是有![]() .化简得
.化简得![]() .
.
解得![]() ,即至少需10年才能把此荒山全部绿化.
,即至少需10年才能把此荒山全部绿化.
(Ⅱ)这10年中,每年所种树苗的木材量(单位:立方米)成等差数列,为200,300,400,…,1100.故所求木材总量S为
![]()
由此可得![]() (立方米).
(立方米).
(21)(Ⅰ)![]() ,设切点为(x0,y0),则
,设切点为(x0,y0),则![]() ,即
,即![]() .
.
又![]() .由此可解得
.由此可解得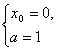 或
或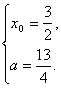
经验证可得![]() 或
或![]() 时,直线
时,直线![]() 是已知曲线的切线.
是已知曲线的切线.
(Ⅱ)![]() .
.
∵ 当![]() 时
时![]() ,
,
∴ 当![]() 时,
时,![]() ,即
,即![]()
∴ 当![]() 时,给出函数在(-1,1)上是减函数.
时,给出函数在(-1,1)上是减函数.
(22)(Ⅰ)设过M点的直线为![]() ,代入
,代入![]() 中可得
中可得![]() ∴ △
∴ △![]() ,解得
,解得![]() ,且
,且![]() .
.
设A(x1,y1),B(x2,y2),则![]() ,则线段AB中点为
,则线段AB中点为![]() ,
,![]() .
.
∴ AB的垂直平分线方程为![]() .令
.令![]() ,得
,得![]() ,即
,即![]() .
.
(Ⅱ)若△![]() 为等边三角形,则点E到AB的距离
为等边三角形,则点E到AB的距离![]() .
.
又![]() ,
,![]()
∴ ![]() .解得
.解得![]() .从而得
.从而得![]() .
.