高三下学期数学模拟试题(三)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的.
(1)a=3是直线![]() 和
和![]() 平行且不重合的( ).
平行且不重合的( ).
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分条件也非必要条件
(2)在等差数列![]() 中,
中,![]() ,
,![]() ,那么其前13项的和
,那么其前13项的和![]() 等于( ).
等于( ).
A.168 B.156 C.78 D.152
(3)已知定点M和定直线l,![]() ,那么经过点M且与直线l相切的动圆的圆心的轨迹是( ).
,那么经过点M且与直线l相切的动圆的圆心的轨迹是( ).
A.直线 B.二条平行直线
C.圆 D.抛物线
(4)已知函数:![]() ,
,![]() ,
,![]() ,
,![]() .从中任取两个相乘得到若干个函数,所得这些函数中偶函数共有( ).
.从中任取两个相乘得到若干个函数,所得这些函数中偶函数共有( ).
A.1个 B.2个 C.3个 D.4个
(5)已知向量![]() 、
、![]() 的夹角为90°,且
的夹角为90°,且![]() ,记
,记![]() ,
,![]() ,若
,若![]() ,则k=( ).
,则k=( ).
A.-6 B.6 C.3 D.-3
(6)若点P在直线![]() 上移动,PA、PB是圆
上移动,PA、PB是圆![]() 的两条切线,A、B是切点,O是原点,则四边形PAOB的面积最小值为( ).
的两条切线,A、B是切点,O是原点,则四边形PAOB的面积最小值为( ).
A.24 B.16 C.8 D.4
(7)点P在曲线![]() 上移动时,过点P曲线的切线的倾斜角的取值范围是( ).
上移动时,过点P曲线的切线的倾斜角的取值范围是( ).
A.![]() ,
,![]() ]
B.[
]
B.[![]() ,p ]
,p ]
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,p )
,p )
(8)从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者都不能从事翻译工作,则选派方案共有( ).
A.280种 B.240种 C.180种 D.96种
(9)已知圆锥轴截面是边长为2的等边三角形,当它的内接圆柱的侧面积最大时,内接圆柱的高为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(10)已知![]() 的展开式中,
的展开式中,![]() 项的系数为100,那么实数a的值为( ).
项的系数为100,那么实数a的值为( ).
A.0或![]() B.
B.![]() 或
或![]() C.0或
C.0或![]() D.
D.![]() ,-
,-![]()
(11)设![]() 是由正数组成的等差数列,
是由正数组成的等差数列,![]() 是由正数组成的等比数列,且
是由正数组成的等比数列,且![]() .若存在自然数m,使得
.若存在自然数m,使得![]() ,则必有( ).
,则必有( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(12)二次函数![]() 的二次项系数为正数,且对任意
的二次项系数为正数,且对任意![]() R都有
R都有![]() 成立,若
成立,若![]() ,则x的取值范围是( ).
,则x的取值范围是( ).
A.![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中空格上.
(13)若双曲线![]() 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为![]() ,则a=________.
,则a=________.
(14)若![]() ,则a=________.
,则a=________.
(15)把正方形ABCD沿对角线BD折成直二面角后,得到的三棱锥A-BCD中,有以下四个结论:
①![]() ;
②△
;
②△![]() 是等边三角形;
是等边三角形;
③AB与面BCD成60°角; ④AB和CD成60°角.
那么以上结论中,正确结论的序号是________.
(16)(理科)一个袋子里有大小相同的3个红球和2个白球,从中同时取出2个,则其中含红球个数的数学期望是________.(用数字作答)
(文科)一个工厂有若干个车间,今采用分层抽样方法从全厂某天的2048件产品中抽取一个容量为128的样本进行质量检查.若一车间这一天生产256件产品,则从该车间抽取的产品件数为________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分12分)
制造某种零件,甲机床的废品率为0.04,乙机床的废品率为0.05,从这二机床生产的产品中各抽出一件作检验,求
(Ⅰ)其中恰有一件废品的概率;
(Ⅱ)其中至多有一件废品的概率;
(Ⅲ)其中没有废品的概率.
(18)(本小题满分12分)
数列![]() 的前n项的和为
的前n项的和为![]() ,且
,且![]() .其中
.其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若数列![]() 是公比为q的等比数列,求证
是公比为q的等比数列,求证![]() ;
;
(Ⅱ)若![]() ,求证数列
,求证数列![]() 是等比数列.
是等比数列.
(19)(本小题满分12分)
正方体![]() 中,E、F分别为AB、BB1的中点(如图综10).
中,E、F分别为AB、BB1的中点(如图综10).
(Ⅰ)证明EF∥平面![]() ;
;
(Ⅱ)求二面角![]() 的平面角的正切值;
的平面角的正切值;
(Ⅲ)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
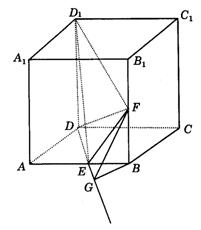
综10
(20)(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求此函数的定义域及单调递增区间;
(Ⅱ)求此函数的极大值和极小值.
(21)(本小题满分12分)
已知甲、乙、丙三种食品的维生素A、B的含量及成本如下表:
| 甲 | 乙 | 丙 | |
| 维生素A含量(单位/千克) | 600 | 700 | 400 |
| 维生素B含量(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
某食品研究所想用x千克甲种食品、y千克乙种食品、z千克丙种食品配制成100千克的混合食品,并使混合食品中至少含有56000单位的维生素A、63000单位的维生素B.
(Ⅰ)用x、y表示这种混合食品的总成本C(元);
(Ⅱ)确定x、y、z的值,使混合食品的总成本最低.
(22)(本小题满分14分)
已知双曲线![]() 的左、右两个顶点分别为A、B,过这双曲线右焦点F2且与x轴垂直的直线交双曲线于两点P、Q、P在x轴上方,且
的左、右两个顶点分别为A、B,过这双曲线右焦点F2且与x轴垂直的直线交双曲线于两点P、Q、P在x轴上方,且![]() ,
,![]() .
.
(Ⅰ)求这双曲线的方程;
(Ⅱ)若直线![]() 与双曲线交于不同两点M、N,且M、N都在以E(0,-1)为圆心的同一个圆上,求k的值.
与双曲线交于不同两点M、N,且M、N都在以E(0,-1)为圆心的同一个圆上,求k的值.
参考答案
一、选择题:
(1)C (2)B (3)D (4)A (5)B (6)C
(7)D (8)B (9)A (10)C (11)B (12)C
提示:
(2)可求得![]() ,公差
,公差![]() .
.
(4)可得6个函数,其中只有![]() 是偶函数.
是偶函数.
(5)由![]() ,得
,得![]() ,即
,即![]() .又
.又![]() ,
,![]() ,
,![]() ,可得
,可得![]() .
.
(6)分析图形知,当![]() 最小时,四边形PAOB面积最小,此时
最小时,四边形PAOB面积最小,此时![]() 为0到已知直线距离.
为0到已知直线距离.
(7)切线斜率![]() ,即
,即![]() 且
且![]() .
.
(8)![]() 或
或![]() .
.
(9)设内楼圆柱底面半径为x,高为h,则![]() ,故
,故![]() .故侧面积
.故侧面积
![]() .当且仅当
.当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
(10)![]() .
.
故![]() .
.
(11)![]() 是
是![]() ,
,![]() 的等差中项,
的等差中项,![]() 是
是![]() ,
,![]() 的等比中项.
的等比中项.
(12)二次函数![]() 的图象向上开口,且以
的图象向上开口,且以![]() 为对称轴,于是有
为对称轴,于是有![]() .
.
二、填空题
(13)3 (14)1 (15)①,②,④ (16)(理科)1、2(文科)16
提示:
(13)双曲线焦点为(0,![]() ),渐近线为
),渐近线为![]() .
.
(16)(理科)取2球其中含红球个数![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
P |
|
|
|
故![]() .
.
(文科)![]() .
.
三、解答题:
(17)设甲机床产品是废品记作A,乙机床产品是废品记作B,则P(A)=0.04,P(B)=0.05
(Ⅰ)![]() .
.
(Ⅱ)![]() .
.
(Ⅲ)![]() .
.
(18)(Ⅰ)∵ 数列![]() 是公比为q的等比数列,且
是公比为q的等比数列,且![]() ,则
,则![]() .
.
∴ ![]() ,即
,即![]() .
.
于是有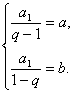 从而可得
从而可得![]() .
.
(Ⅱ)若![]() ,故
,故![]() .
.
当n=1时,![]() ,
,
当![]() 时,
时,![]() .又当
.又当![]() 时,
时,![]() ,∴
,∴![]() N*).
N*).
∴ 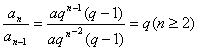 ,即
,即![]() 是等比数列.
是等比数列.
(19)(Ⅰ)∵ E、F分别是AB和BB1的中点,∴![]() ,又EF在平面
,又EF在平面![]() 上,
上,![]() 在平面
在平面![]() 上,∴ EF∥平面
上,∴ EF∥平面![]() .
.
(Ⅱ)过B在平面ABCD由作![]() 于G,连结FG.由于
于G,连结FG.由于![]() 平面ABCD,∴
平面ABCD,∴![]() ,故
,故![]() 为二面角
为二面角![]() 的平面角.
的平面角.
设正方体棱长为2a,在Rt△![]() 中,
中,![]() .
.![]() .
.
∴ ![]() .
.
在Rt△![]() 中,
中,![]() .
.
(Ⅲ)∵ ![]() 平面
平面![]() ,
,
∴ ![]() .
.

答10
(20)(1)函数定义域为![]() .
.
![]() ,得
,得![]() 或
或![]()
∴ 函数的单调递增区间为(-1,0),(1,+![]() ).
).
(2)列表:

∴ 函数的极小值为![]() 或
或![]() ,没有极大值.
,没有极大值.
(21)(Ⅰ)依题意有![]() .
.
![]() .
.
(Ⅱ)![]() 中把
中把![]() 代入,可得
代入,可得![]()
∴ ![]()
当且仅当![]() 即
即![]() 时上式等号成立
时上式等号成立
∴ 当![]() 千克,
千克,![]() 千克,
千克,![]() 千克时,混合食品总成本最低.
千克时,混合食品总成本最低.
(22)(Ⅰ)由已知可求得P(c,![]() ),故在Rt△
),故在Rt△![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() .
.
又![]() ,
,![]() .
.
∴ ![]() ,解得
,解得![]() ,∴ 双曲线方程为
,∴ 双曲线方程为![]() .
.
(Ⅱ)把![]() 代入
代入![]() 中,可得
中,可得![]() .
.
∴ 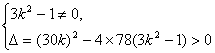 ①
①
此时设![]() ,
,![]() ,N
,N![]() ,
,![]() ,则
,则![]() .
.
∴ MN中点F的坐标为![]() .
.
由![]() ,故
,故![]() ,即
,即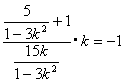 ,解得
,解得![]() .
.
经验证,![]() 符合①,因此
符合①,因此![]() 为所求.
为所求.