高三下学期数学模拟试题（一）

高三下学期数学模拟试题（一）

　　一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

　　（1）已知全集U＝R，集合，，则（）∪（）＝（　）．

　　A．　　　　　　　　　　　 B．

　　C．　　 　　　　　　　　 D．或

　　（2）函数是（　）．O

　　A．周期为π的偶函数　 　　　　　　 B．周期为π的奇函数

　　C．周期为1的偶函数　 　　　　　　 D．周期为1的奇函数

　　（3）已知空间四边形的四边长都相等，那么顺次连结各边中点的四边形一定是（　）．

　　A．梯形　　　　B．菱形　　　　C．矩形　　　　 D．正方形

　　（4）函数的反函数是（　）．

　　A． 　　　　　B．

　　C．　 　　　　　　 D．

　　（5）抛物线的准线方程是（　）．

　　A． 　 B．　 　　C． 　　　D．

　　（6）已知，，则下列不等式中一定成立的是（　）．

　　A． 　　　　　　　　　 B．

　　C．　　　　　　　  　　D．

　　（7）若向量（1，1），（1，－1），（－1，2），则（　）．

　　A． 　　　　　　　　　　B．

　　C．　　　　　　　　　　　 D．

　　（8）的展开式中，常数项是（　）．

　　A．第4项 　　 B．第5项　 　 C．第6项　　　 D．第7项

　　（9）从数字1，2，3，4，5中任取两个不同的数字构成一个两位数，则这个两位数大于40的概率是（　）．

　　A． 　　　　 B．　　　　　C． 　　　　　D．

　　（10）曲线在点 处的切线的倾斜角是（　）．

　　A．45°　　　　B．135° 　　　C．30°　　　　 D．150°

　　（11）等差数列中，若，则＝（　）．

　　A．－8 　　　　B．20　　　　　C．22　　　　　 D．24

　　（12）在正三棱锥中，M、N分别是侧棱PB、PC的中点，若截面侧面PBC，则此三棱锥的侧棱与底面所成角的正切值是（　）．

　　A． 　　　 B．　　　　 C．　　　　 D．

　　二、填空题：本大题每小题4分，共16分，把答案填在题中横线上．

　　（13）直线与两坐标轴所构成的三角形的面积为，则＝________．

　　（14）＝________．

　　（15）如果复数，那么z的三角形式是________．

　　（16）正方体的对角线长为l，那么它的体积为________．

　　三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤．

　　（17）（本小题满分10分）

　　已知，，}，求的值．

　　（18）（本小题满分10分）

　　已知，），，），求与的夹角的值．

　　（19）（本小题满分12分）

　　已知等比数列中，，，求及前6项和．

　　（20）（本小题满分14分）

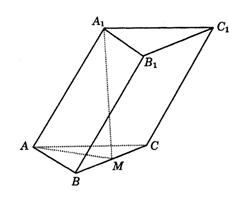
　　如图综7，三棱柱中，，90°，顶点在底面ABC上的射影为BC边的中点M．

　　（Ⅰ）求证：BC垂直于过三点A₁、A、M的平面；

　　（Ⅱ）如果平面与平面ABC所成的二面角为60°，求三棱柱的体积．

　　（21）（本小题满分14分）

　　设函数的图象与y轴的交点为P，且曲线在P点处的切线方程为．若函数在x＝2处取得极小值－16．

　　（Ⅰ）求函数的解析式；

　　（Ⅱ）确定函数的单调减小区间．

　　（22）（本小题满分14分）

　　已知双曲线的离心率，过点A（0，－b）和B（a，0）的直线与原点间的距离为．

　　（Ⅰ）确定这个双曲线的方程；

　　（Ⅱ）直线与双曲线交于两个不同的点C、D，并且C、D两点都在以A为圆心的同一个圆上，求实数m的取值范围．

参考答案

　　一、选择题：

　　（1）D　　 （2）D　　 （3）C　　 （4）C　　 （5）D　　 （6）C

　　（7）A　　 （8）B　　 （9）B　　 （10）A　　（11）B　　（12）C

　　提示：

　　（3）注意此时空间四边形两对角线互相垂直．

　　（4）给出函数的值域为．

　　（5）先把抛物线方程化成标准方程

　　（9）．

　　（10），故．

　　（11）设等差数列公差为d，由已知可得，而．

　　（12）依条件可知PA＝AB，因此取BC中点E，连结PE，交MN于H，则AH是PE的垂直平分线．

　　二、填空题：

　　（13）　　（14）－2　　（15）　　（16）．

　　提示：

　　（14）．　　  ．

　　（15）．

　　三、解答题：

　　（17）∵　，，，∴　，．

　　　 ∴　．

　　（18）由已知，，1），，2），

　　∴　，．

　　∴　，．

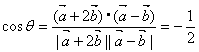　　（19）设等比数列公比为q，则，．解得，．

　　∴　，．

　　（20）（Ⅰ）连结、，∵　M是在平面ABC上面的射影，

　　∴　平面ABC，平面ABC，∴　BC．

　　由　AB＝AC，M是BC中点，有．

　　∴　平面．

　　（Ⅱ）过M作于N，连结，故，

　　∴　是平面与平面ABC所成二面角的平面角，

　　∴　＝60°．

　　在Rt△中，，．

　　在Rt△中，60°

　　∴　．

　　（21）（Ⅰ），则．

　　又直线的斜率为－24，故C＝－24．

　　把代入，得．故P（0，12）．由此可得．

　　∴　．

　　由在处取极小值－16，得

　　解得

　　∴　．

　　（Ⅱ），令，得．

　　∴　的单调减区间是（－4，2）．

　　（22）（Ⅰ）由有，即．过A、B的直线方程为，依题意有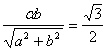．由此解得，．∴　双曲线方程为．

　　（Ⅱ）把代入中，可得．

　　故，．①设C（x₁，y₁）、D（x₂，y₂），则，．

　　∴　CD中点P的坐标为，．由已知则有，而A（0，－1）．于是有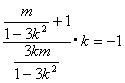，化简得．　　　　　　　　　　　　　　　 ②

　　②代入①，得，，又，则．解得或．