高三数学十校联考试卷
数学
|
、S分别表示上、下底面积，h表示高三角函数的和差化积公式
第I卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只
有且只有一项是符合要求的．
1．函数
的图象是 （ ）
（A）圆的一部分 （B）抛物线的一部分
（C）椭圆的一部分 （D）双曲线的一部分
2．把复数1+i对应的点向右平移一个单位，再向下平移一个单位得到点A，把所得的向量
按逆时针方向旋转120°，得到向量
，则B点对应的复数为 （ ）
（A）
（B）0
（C）
（D）
3．（理）同时满足下列四个条件中的2个，其中与
等价的是 （ ）
（1）
（2）
（3）
（4）
（A）（1）（2） （B）（1）（3）或（3）（4）
（C）（1）（2）或（3）（4） （D）（2）（3）或（3）（4）
3．（文）同时满足下列三个条件中的2个，其中与等价的是 （ ）
（1） （2）
（3）
（A）（1）（2） （B）（1）（3） （C）（2）（3） （D）不可能
4．奇函数
有反函数
则必在
的图象上的点是（ ）
（A）
（B）
（C）
（D）
5．发电厂发出的电是三相交流电，它的三根导线上的电流强度分别是关于时间t的函数：
且IA+IB+IC=0，
，则
=（ ）
（A）
（B）
（C）
（D）
6．三棱锥A—BCD中，AB=AC=BC=CD=AD=a，要使三棱锥A—BCD的体积最大，则二
面角B—AC—D的大小为 （ ）
（A）
（B） （C） （D）
7．（理）在极坐标系下，极坐标方程
表示的曲线与点
的位置关
系是 （ ）
（A）在曲线内 （B）在曲线外 （C）在曲线上 （D）与ρ、θ有关
8．（理）（7文）将7个相同的白棋子与3个相同的黑棋子排成一排,共有不同的排法种数是
（ ）
（A）720 （B）210 （C）120 （D）35
|
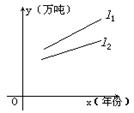
直线l1表示该化肥在各年的年产量：直线l2表示该
化肥各年的销售情况。根据所学知识，你认为下列
叙述较为合理的是 （ ）
（1）该化肥产量、销售量均以直线上升，仍可按
原生产计划进行下去；
（2）该化肥已经出现了供大于求的情况 ，价格将趋跌；
（3）该化肥的库存积压将越来越严重，应压缩产量或扩大销售量；
（4）该化肥的产、销情况均以一定的年增长率递增。
（A）（1）（2）（3）（B）（1）（3）（4） （C）（2）（4） （D）（2）（3）
10．（理）（文9）已知反比例函数
的图象是等轴双曲线，则其焦点坐标是 （ ）
（A）
（B）
（C）
（D）
10．（文）现行足球赛的计分规则是：胜一场，得3分，平一场，得1分，负一场，得0分．
某球队踢完8场，积19分，若不考虑胜、负、平的顺序，该队胜、负、平的情况共有：
（A）1种 （B）2种 （C）3种 （D）6种
|
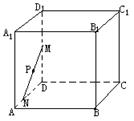
∠BAD=60°，长为2的线段MN的一个端点M在DD1
上运动，另一个端点N在底面ABCD上运动。则MN中
点P的轨迹与直平行六面体的面所围成的几何体的体积
为 （ ）
（A）
（B）
（C）
（D）
12．已知数列
的通项公式为
则关于an的最大、最小项叙述正
确的是 （ ）
（A）最大项为a1，最小项a3 （B）最大项为a1，最小项不存在
（C）最大项不存在，最小项为a3 （D）最大项a1，最小项a4
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题有4小题，每小题4分，共16分．请将答案填在题中的横线上．
|
有相等的实根，则点（a，b）
的轨迹的焦点坐标是 ．
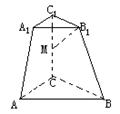
14．如图，三棱台ABC—A1B1C1中，CC1=2A1C1=2B1C1=a，∠ACB=90°
CC1⊥底面ABC，M是CC1的中点，则AB与B1M所成的角为
．
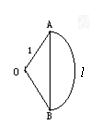
15．（文）已知如图，扇形弧长为
，半径为1，则△AOB
|
15．（理）（文16）已知数列满足a1=1，当n≥2时，
则
的通项公式为
（写出你认为正确的一个答案即可）．
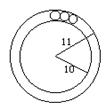
16．（理）如图表示一滚珠轴承过珠心的截面，其图形为一个圆环，
该圆环的内、外半径分别为10cm与11cm，滚珠的直径为1cm，
则这个轴承应配的滚珠数为 的整数部分．（用反正弦表示）
三、解答题：本大题有6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）已知函数
（1）要得到
的图象，只需把
的图象经过怎样的平移或伸缩变换？
（2）求
的最大值及相应的x．
18．（理）（本小题满分12分）已知数列中，
是
的前n项和，又
如果b≠0，求
18．（文）（本小题满分12分）已知数列中，
是
的前n项和，又如果a≠0，求
19．（理）（本小题满分12分）已知
为偶函数，在
上是增函数，试解关于x
的不等式；
其中k＞0．
19．（文）（本小题满分12分）已知为偶函数，在上是增函数，试解关于x
的不等式；其中k≥1．
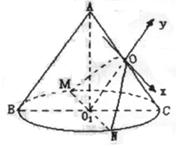
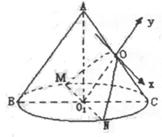
20．（本小题满分12分）已知圆锥的侧面展开图是一个半圆，它被过底面中心O1且平行于
母线AB的平面所截，若截面与圆锥侧面的交线是焦参数（焦点到准线的距离）为p的
|
（1）求圆锥的母线与底面所成的角；
（2）求圆锥的全面积．
21．（本小题满分12分）医学上为研究传染病传播中病毒细胞的发展规律及其预防，将病
毒细胞注入一只小白鼠体内进行实验，经检测，病毒细胞的增长数与天数的关系记录
如下表。已知该种病毒细胞在小白鼠体内的个数超过108的时候小白鼠将死亡．但注射
某种药物，将可杀死其体内该病毒细胞的98%．
（1）为了使小白鼠在实验过程中不死亡，第一次最迟应在何时注射该种药物？（精确
到天）
（2）第二次最迟应在何时注射该种药物，才能维持小白鼠的生命？（精确到天）
|
22．（理）（本题满分14分）已知椭圆C的中心在原点，焦点F1、F2在x轴上，点P为椭圆
上的一个动点，且∠F1PF2的最大值为90°，直线l过左焦点F1与椭圆交于A、B两点，
△ABF2的面积最大值为12．
（1）求椭圆C的离心率；
（2）求椭圆C的方程．
22．（文）（本题满分14分）已知椭圆C的中心在原点，焦点F1、F2在x轴上，点P为椭圆
上的一个动点，且∠F1PF2的最大值为90°，直线l过左焦点F1倾斜角为45°，与椭
圆交于A、B两点，△ABF2的面积最大值为12．
（1）求椭圆C的离心率；
（2）求椭圆C的方程．
2002年宁波市十校联考数学试卷参考答案
一、选择题（每小题5分，共60分）
1．D 2．A 3．B 4．B 5．C 6．A 7．A （文7C） 8．C（文8D） 9．D（文9A） 10．A 11．B 12．A
二、填空题（每小题4分，共16分）
13．（0，1） 14．60° 15．
或
中的一个（文15、
） 16．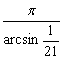
等价答案为：
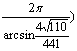（文16、或中的一个即可）
三、解答题：本大题有6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）
解：（1）
……………………（4分）
所以要得到
的图象只需把
的图象向左平移
即可．
（注：等价答案同样给分）…………………………………………………………（6分）
（2）
……（10分）
当
即
时，
取得最大值
…………………（12分）
18．（理）（本小题满分12分）
解：
………………………………………………（2分）
……（8分）
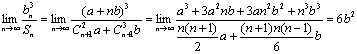………………（12分）
18．（文）（本小题满分12分）
解：
……（2分）
……………………（8分）
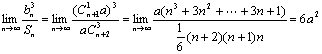………………（12分）
另解：
………………………………………………（2分）
（8分）
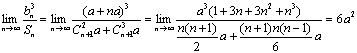……………………（12分）
19．（理）（本小题满分12分）
解：由题意为偶函数，在上是增函数，
得：
………………（4分）
……（7分）
∴当k=1时，x＜0………………………………（8分）
当k＞1时，
……（10分） 当0＜k＜1时，x＜0或
（12分）
19．（文）（本小题满分12分）
解：由题意为偶函数，在上是增函数，
得：………………（4分）整理得
……（8分）
∴当k=1时，x＜0 当k＞1时，……（12分）
20．（本小题满分12分）
|
由题意得：
即
所以母线和底面所成的角为60°……（4分）
（2）设截面与圆锥侧面的交线为MON，其中O为截面与
AC的交点，则OO1//AB且
……（6分）
在截面MON内，以OO1所在有向直线为y轴，O为原点，建立坐标系，则O为抛物的顶点，所以抛物线方程为x2=－2py，点N的坐标为（R，－R），代入方程得
R2=－2p（－R），得R=2p，l=2R=4p……………………………………………………（9分）
∴圆锥的全面积为
…………………………（12分）
21．（本题满分12分）
解：（1）由题意病毒细胞关于时间n的函数为
…………………………………（3分）
则由
两边取对数得
即第一次最迟应在第27天注射该种药物……………………………………………………………………………（5分）
（2）由题意注入药物后小白鼠体内剩余的病毒细胞为
………………（7分）
再经过x天后小白鼠体内病毒细胞为
…………………………（9分）
由题意≤108，两边取对数得
，
即再经过6天必须注射药物，即第二次应在第33天注射药物．…………（12分）
22．（理）（本题满分14分）
解：（1）设
由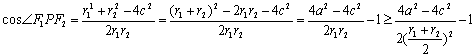
得
（注：根据几何直观并给出适当说明得出离心率的酌情给分）……（6分）
（2）①当k存在时，设l的方程为
………………①
椭圆方程为
由得
于是椭圆方程可化为
………………②
把①代入②得：
整理得
…………………………（8分）
则x1、x2是上述方程的两根．
且
|
AB边上的高
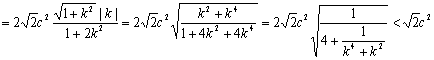…（12分）
②当k不存在时，把直线
代入椭圆方程
得
由①②知S的最大值为
由题意得
=12 所以
所以面积最大时椭圆方程为：
………………………………（14分）
另解：设过左焦点的直线方程为：
…………①
椭圆的方程为：
由
得：
于是椭圆方程可化为：
……②
把①代入②并整理得：
…………………………（8分）
于是
是上述方程的两根。
AB边上的高
所以
当且仅当m=0取等号……………（12分） 由题意知
得：
所以面积最大时椭圆方程为：…………（14分）
22．（文）（本题满分14分）（1）同理（1）答案
（2）设l的方程为
……①椭圆的方程为
由得：于是椭圆方程可化为：
……②（8分）
把①代入②得：
………………（10分）
…………（12分）
得c2=9 a2=18 b2=9
∴椭圆方程为
……………………（14分）