高三数学期末统测模拟试卷

高三数学期末统测模拟试卷

一、选择题

1、若P、Q为两个非空实数集，定义集合P+Q={a+ba∈P，b∈Q}，若P={0，2，5}，Q={1，2，6}，则P+Q中元素的个数是：

　A、9　　　　　　　　　　　B、8　　　　　　　　　　　　　 C、7　　　　　　　　　　　　　D、6

2、对任意实数a、b、c，给出下列命题：

　①“a=b”是“ac=bc”的充要条件；

②“a+5是无理数”是“a是无理数”的充要条件；

③“a＞b”是“a²＞b²”的充分条件

④“a＜5”是“a＜3”的必要条件

其中真命题的个数是：

A、1　　　　　　　　　　　B、2　　　　　　　　　　　　　 C、3　　　　　　　　　　　　　D、4

　　　　　　　　　　　　　　x－2＜2

3、不等式组　　　　　　　　　　　　　　　　　的解集为：

　　　　　　　　　　　　　　log₂(x²－2)＞1

　A、（0，）　　　 B、（，2）　　　　　 C、（，4）　　　　　 D、（2，4）

4、对任意的锐角α、β，下列不等式关系中正确的是：

　A、sin(α+β)＞sinα+sinβ　　　　　　　　　　B、cos(α+β)＜sinα+sinβ

C、sin(α+β)＞cosα+cosβ　　　　　　　　　D、cos(α+β)＜cosα+cosβ

5、函数y=Asin()(＞0，＜，x∈R)的部分图象如图所示，则函数表达式为：

　A、

B、

C、

D、

6、已知向量、、，且++=，=3，=4，=5，设与的夹角为θ₁，与的夹角为θ_2­，与的夹角为θ₃，则θ₁、θ₂、θ₃的大小关系是：

　A、θ₁＜θ₂＜θ₃　　　　　　　　　　　　　　 B、θ₁＜θ₃＜θ₂　　

C、θ₂＜θ₃＜θ₁D、θ₃＜θ₂＜θ₁　　

7、已知数列{a­­_n}满足a₁=0，(n∈N⁺)，则a₂₀=

　A、0　　　　　　　　　　　B、－　　　　　　C、　　　　　　　　D、

8、设f(x)是定义在R上以6为周期的函数，f(x)在(0，3)内单调递减，且y=f(x)的图象关于直线x=3对称，则下面正确的结论是：

　A、f(1.5)＜f(3.5)＜f(6.5)　　　　　　　　　 B、f(3.5)＜f(1.5)＜f(6.5)

C、f(6.5)＜f(3.5)＜f(1.5)　　　　　　　　　 D、f(3.5)＜f(6.5)＜f(1.5)

9、在y=2^x，y=log₂x，y=x²，y=cos2x这四个函数中，当0＜x₁＜x₂＜1时，使＞恒成立的函数的个数是：

　A、0　　　　　　　　　　　B、1　　　　　　　　　　C、2　　　　　　　　　 D、3

10、若函数f(x)=log_a(2x²+x)(a＞0，a≠1)，在区间(0，)内恒有f(x)＞0，则f(x)的单调递增区间为：

　A、(－∞，－)　　　　　　　　　　　　　　　B、(－，+∞)

C、(0，+∞)　　　　　　　　　　　　　　　　　　　D、(－∞，－)

11、探索以下规律：0 → 3 → 4 → 7 → 8 → 11 → ……

 

1 → 2  　 5 →6　  9 → 10

则根据规律，从2002到2004，箭头的方向依次为：

A、→ 　　　　　　　　　B、→　　　　　　　　　C、→　　　　　　　　 D、→

12、在等差数列{a­_n}中，若它的前n项之和S_n有最大值，且＜－1，那么当S_n是最小正数时，n的值为：

　A、1　　　　　　　　　　　B、18　　　　　　　　　C、19　　　　　　　　 D、20

二、填空题

13、若sin(－θ)=，则sin2θ=___________

14、在“”中的“__  __”处分别填上一个自然数，并使他们的和最小。

15、数列{a­_n}中a₁=1，前n项和S_n满足S_n=(1+)²(n∈N₊，且n≥2)，且通项公式a_n=_______________

16、已知定义在R上的奇函数f(x)，当x＞0时，f(x)＞0，f '(x)＞0，f(3)=，则不等式x·f(x)＜1的解集是_______________

17、规定记号“*”表示一种运算。

即a*b=+a+b(a、b∈R⁺)，若1*k=3，则函数f(x)=k*x的值域是______________。

18、已知函数f(x)=ax³+3x²－x+1在(－∞，+∞)上单调增函数，则a的取值范围是_______________________。

三、解答题

19、已知P：1－≤2，Q：x²－2x+1－m²≤0(m＞0)，若 P是 Q的充分而不必要条件，求实数m的取值范围。

20、已知△ABC三内角A、B、C成等差数列，=(1+cos2A，－2sinC)，=(tanA，cosC)

（1）若⊥，判断△ABC的形状；

（2）求·取最大值时，△ABC三内角的大小。

21、某地区发生流行性病毒感染，居住在该地区的居民必须服用一种药片预防，规定每人每天上午8时和晚上20时各服一片。现知该药片每片含药量为220毫克，若人的肾脏每12小时从体内滤出这种药的60%，该药物在人体内的残留量超过380毫克，就将产生副作用。

（1）某人上午8时第一次服药，问到第二天上午8时服完药后，这种药性在他体内还残留多少？

（2）若人长期服用这种药，则这种药会不会对人体产生副作用？说明理由。

22、下表给出一个“三角形数降”：

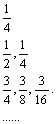
已知每一列的数成等差数列，从第三行起，每一行的数成等比数列，每一行的公比都相等，记第i行第j列的数为a_ij（i≥j，i、j∈N₊）

（1）求a₈₃；

（2）试写出a_ij，关于i、j的表达式；

（3）记第n行的和为A_n，求数列{A_n}的前m项和B_m的表达式。

23、已知函数y=f(x)=x³－x+a，（x∈[－1,1]　a∈R）

（1）求函数f(x)的值域；

（2）设函数y=f(x)的定域为D，共时任意的x₁、x₂∈D都在f(x₁)－f(x₂)＜1成立，则函数y=f(x)为“标准函数”否则称为“非标准函数”。试判断函数f(x)=x³－x+a（x∈[－1,1]　 a∈R）是否为“标准函数”，如果是，请给出证明，如果不是，请说明理由。