高三数学全程复习（一轮）

高三数学全程复习（一轮）

课时08 函数的值域

【考点指津】

1．理解函数值域的概念，掌握求函数值域的各种方法．

函数的值域就是函数值的集合，它取决于函数的定义域和对应法则．

求函数值域的基本方法有：数形结合法、反函数法、配方法、判别式法等，应弄清各方法所适用的函数类型．

2．掌握常见函数的最值的求法．

函数的最值就是函数的最大值或最小值．若函数的最大值与最小值分别为M与m，则函数的值域为[m，M]或它的真子集．

解决函数最大（小）值问题的依据有：函数的性质、不等式的性质、函数与几何图象的性质．

求函数的最值方法包括单调性法、基本不等式法、换元法、配方法、图象法等．

【知识在线】

1．函数的值域为　　　　．

2．已知函数y = log₂(x²-2)的值域是[1，log₂14]，则此函数的单调减区间为　　　 ．

3．函数的值域为　　　 （　）

A．[-1，0]　　　 B．（-1，0）　　　　C．[-1，0]　　　 D．[0，1]

4．已知集合A=｛y︱y=2^x， x∈R｝ B=｛y︱y=x² ，x∈R｝则　　　　　  （　）

A． A∩B=｛2 ，4｝ 　B． A∩B=｛4 ，16｝  C． A=B　　D．AB

5．定义域为R的函数y = f(x)的值域为[a，b]，则f(x+a)的值域为　 　　　 （　）

　　　 A．[2a，a+b]　　　 　　B．[0，b-a]　　　　　 C．[a，b]　　　　　 D．[-a，a+b]

【讲练平台】

　　　 例1　求下列函数的值域：

　　　 （1）；

（2）；

（3）．

分析　（1）先对表达式进行化简，后利用反函数法或观察法求值域；（2）将其转化为含有参数y的关于x的方程，利用“判别式”法求解；（3）先换元，得到新变量的一元二次函数，再求其值域，或利用函数的单调性求值域．

解　（1）　（x≠1）．

解法一（反函数法） 由函数y = ，得．

解不等式≠1，且≠ -3，得

　　　 y≠，且y≠2．

故函数的值域为{yy∈R，且y≠，y≠2}

解法二（观察法） y = ．

由于x≠1，且x≠ -3，故x+3≠4，且x+3≠0，从而，y≠，且y≠2．

故函数的值域为{yy∈R，且y≠，y≠2}

（2）由，得yx²-(y+1)x+y=0，这是一个关于x的方程．

当y=0时，解得x=0，方程有解；

当y≠0时，为使关于x的二次方程有解，必须△= (y+1)² - 4y²≥0，解得

≤y≤1（y≠0）．

综合得，函数的值域是[，1]．

（3）解法一　令t=，得 x=1-t²，于是y= g(t)=1-t²-t（t≥0）．

配方，得 y= g(t) = - (t+)²+，它在为减函数，故最大值为g(0)=1，于是，所求函数的值域是（-∞，1 ]．

解法二　易知函数的定义域为（-∞，1 ]，而且该函数在定义域内为减函数，故最大值为f(1) = 1，从而所求函数的值域为（-∞，1 ） ．

点评　（1）求函数值域有很多方法，每种方法又各有其适用类型，要根据函数式的特征准确选用相应的方法：上述各小题的解法分别使用了反函数法（反函数的定义域就是原函数的值域）、观察法（形如(a≠0)的函数的值域为{yy∈R，且y≠}）、判别式法及换元法与单调性法；

（2）在用判别式法求值域时，如果得到的关于x的方程的二次项系数中含有字母y，则应分情况讨论．例如，求函数的值域，变形得到方程yx²-yx+(y-1)=0，易见，当y=0时，方程无解；当y≠0时，由△≥0，解得 0≤y≤（y≠0）．故值域为]，而不是[0，]；

（3）利用换元法解题时，必须注意变量的等价性，如题（3）中新变量t的取值范围为t≥0，若忽视了这一点，可能导致错误的答案为y≤；

（4）函数（2）亦可用不等式法求值域．当x = 0时，y = 0；当x≠0时， y =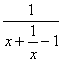，因≥1，或≤-3，故≤y≤1（y≠0）．于是，函数的值域为[，1] ．

　　　 变题　已知函数y = 的值域为[1，9]，试求函数y=的值域．

　　　 提示：将y = 变形为(y – a)x² –8x+ y – b=0，利用“△≥0”可得

　　　　　　　y² – (a+b)y+ab-16≤0．

　　　 它与不等式(y-1)(y-9) ≤0，即y²-10y+9≤0等价，比较系数得

　　　　　　　a = b = 5．

　　　 y==≥．

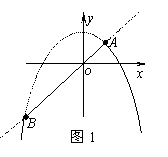
例2　已知函数f(x)=2-x²，g(x)=x．若f(x)*g(x)=min{f(x)，g(x)}，那么f(x)*g(x)的最大值是　 　　　．（注：min表示最小值）

分析　这是一道信息题，应将表达式f(x)*g(x)=min{f(x)，g(x)}进行展开，得到分段函数后，画出图像，根据图像得出所求的最大值．

解　y=f(x)*g(x) ．

画出上述函数的图像，如图1的实线部分，由图易知，图中的最高点A的纵坐标即为所求．

解方程组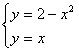，得

(x，y) = (1，1)或（-2，-2）．

于是所求的最大值为1．

点评　（1）分段函数的最值一般均用图像法画出各分段函数的图像，然后观察（求）出它们在各段图像上的最值点，并比较它们最值的大小；

（2）容易误认为所求的最大值就是函数f(x)的最大值或g(x)的最大值；

（3）不能认为 –2是的最小值．

变题　已知函数f(x)=2-x²，g(x)=x．若F(x)= f(x)*g(x)= max{f(x)，g(x)}，那么F(x)是否存在最小值．请说明理由．

答案：不存在最小值．（注：只存在极小值1，极大值2）

例3　已知函数f(x)=．

　　　 （1）当a=0.5时，求函数f(x)的最小值；

　　　 （2）当a= 4时，求函数f(x)的最小值．

　　　 分析　这是一个带有定义域的分式函数求最值问题，能否使用算术几何平均值不等式求最值，要视a的取值而定．因为用算术几何平均值求最值的条件是“一正二定三相等”，这里的相等条件能否成立是一个关键．

解　（1）当a =0.5时，f(x)=x++2， ．

任设1≤x₁＜x₂，则

f(x₁) - f(x₂) =( x₁++2)-( x₂++2)=

因1≤x₁＜x₂，故x₁- x₂＜0，且x₁x₂＞1，于是x₁x₂＞0，2x₁x₂-1＞0，从而f(x₁) - f(x₂)＜0，即f(x₁) ＜ f(x₂)，故f(x)在上是增函数，所以f(x)在上的最小值是f(1)=．

　　　 （2）≥，

当且仅当，即x=2∈[1，+∞）时，取“=”，

故函数的最小值为6．

点评  （1）求函数值域（最值）方法很多，单调性法是重要方法之一．当诸多方法失效时，单调性法往往奏效；

（2）对于题（1），不能用判别式法求最小值．事实上，由y=x++2得2x²-2(y-2)x +1=0，由△= 4(y-2)²-8≥0得 y≥2+(因y＞0，故y≤2-，不合，舍去．)．这时若认为y_min=2+那就错了．因为当y=2+时，2x²-2x+1=0，解得x=；也不能用算术几何平均值不等式求最值．事实上，y=x++2=2+，取等号的条件是x=，即x=，但，故该法也是失效的．

　　　 变题1　求函数f(x)=的最小值，其中a为常数，且a＞0．

　　　 答案：f_min(x) =

　　　 变题2　求函数（a为正常数）的最小值．

　　　 答案：．

例4　已知函数f(x)= 　m，n∈R．

（1）若m∈N*，x∈R， 且f(x)的值域为[1，2]，求m，n的值；

（2）若n= -1，且f(x)的值域为R，求m的取值范围．

分析　（1）先“脱”去对数符号，即变为一个分式函数的值域为[2，4]，可利用“判别式”法及根与系数的关系，求m，n的值；（2）对数函数的值域为R，等价于真数能取遍一切正实数，即真数的最小值应为非正数，同样也可以使用“判别式”法加以求解．

解　（1）设y= ， 由已知，得2≤y≤4．

将分式变形为　myx²+y=3x²+2x+n，

即　 (3-my)x²+2x+n-y=0．

故　 △=4-4(n-y)(3-my)≥0，

即　 my²-(3+mn)y+3n-1≤0 ．　　 

因　2≤y≤4，

故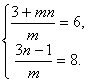　　 

解得　m=1，n=3．（m = ，n = ，不合，舍去．）

（2） ①m=0时，f(x)=∈R；

 ②m≠0时，要使f(x)∈R，只须的值域包含（0，+∞），即．

设y= ，即(3-my)x²+2x-1-y=0，从而

△= -4[my²-(3-m)y-4]≥0，

　　　 即　my²-(3-m)y-4≤0．

要使函数的值域包含（0，+∞），只须m＜0时，且方程有两个负根（相等或不等），故

Þ　 Þm≤-9 或-1≤m＜0．

综上所述，m的取值范围为：m≤-9 或-1≤m＜0．

点评　函数f(x) = log_ag(x)的值域为R（其中x∈R，g(x) = mx²+nx+p，m≠0，m、n、p∈R，a∈(0，1)∪(1，+∞)）Û（0，+∞）Í{g(x) x∈R} Û函数g(x)的最小值不大于0Û存在x₀∈R ，使得g(x₀) ≤0Û△≥0，且m＞0．

【知能集成】

　　　 1．设函数f(x)存在最大值M与最小值m，λ为待求常数．

　　　 （1）若对定义域内的任一x，都有λ≥f(x)，则λ≥M；

（2）若对定义域内的任一x，都有λ≤f(x)，则λ≤m；

（3）若存在x₀，使得f(x₀) ≥λ，则λ≤M；

（4）若存在x₀，使得f(x₀) ≤λ，则λ≥m．

2．掌握函数与方程的思想．

函数与方程的思想就是，先构造函数，把给定问题转化为所构造函数的性质研究后，得出所需的结论．方程思想，就是把对数学问题的认识，归纳为对方程或方程组的认识．

【训练反馈】

1．函数y= 的值域是 　　　　　 ．

2．若函数y=f(x)的值域是[-2，3]，则函数y=∣f(x)∣的值域是　　　　　　 （　）

  A．[-2，3]　　B．[2，3]　　 C．[0，2]　　D．[0，3]

3．函数y=x+的值域是　　　　　　　　　　　　　　　　　　　　  （　）

 　 A．{yy≥}　B．{yy≤}　 C．{yy≥0}　 D．{yy≤0}

4．下列函数中，值域是（0，+∞）的是　　　　　　　　　　　　　　　  （　）

　　　 A．y=2x+1（x＞0）　　　　　　　　 B．

　　　 C．y = x² +x+1　　　　　　　　　　  D．y =

5．凸函数的性质定理为：如果函数f(x)在区间Ｄ上是凸函数，则对于区间Ｄ内的任意x₁，x₂，……，x_n，有

≤f()．

　　　 已知函数y＝sinx在区间（０，π）上是凸函数，则在△ABC中，sinA＋sinＢ＋sinC的最大值为______．

6．当x≤1时，函数f(x)=ax+2a+1的值有正也有负，则实数a的取值范围为　　　　 ．

7．已知函数f(x)的值域为[，16]，求函数g(x)= f(x)+2及h(x) = f(x) -2的值域．

8．设周长为a (a＞0)的等腰三角形，其腰长为x，底边长为y，试将y表示为x的函数，并求出这个函数的定义域和值域．

9．求下列函数的值域：

（1）　　　 y= ；（2）y= ；（3）y= ；（4）y=x+2．

10．若函数的定义域和值域都是[1，b] (b＞1)，求b的值．

11．在区间上，函数在同一点取得相同的最大值，求f(x)在区间上的最小值．

12．已知函数的定义域为R；

（1）求实数m的取值范围；

（2）当m变化时，若y的最小值为f(m)，求函数f(m)的值域．

参考答案：

【知识在线】

1． [0，3 ]　　2． [-4，-2]　　　 3．A　　4．D　　5．C

【训练反馈】

1．[0，]　 2．D　 3．A　 4．B　 5．提示：sinA＋sinＢ＋sinC≤3sin()=3sin60º=　 6．提示：显然a≠0，故函数为单调函数，从而f(-1)·f(1)＜0，解得：-1＜a＜- ．　7．提示：令t= f(x)，则g(x) = G(t)= t+2，G(t)在[，16]上为增函数，值域为[，24]．h(x) = H(t) = t - 2= (- 1)² –1∈[-1，8]．　 8．y= a – 2x，定义域为（，），值域为（0，）． 9．提示：（1）利用观察法或分式变形可得，{y∣y≠2}；（2）求出x²关于y的表达式，解不等式x²≥0得，{y-1≤y＜1}；（3）去分母后利用判别式法可得，[-1，]；（4）利用换元法化为一元二次函数，再利用配方法可得，{yy≤2}．　　10．提示：由函数图象的对称轴方程为x=1，得函数在[1，b]上为增函数，故有f(1)=1，f(b)=b，解得b=3（b=1不合，舍去）

11．提示：g(x)=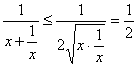，当且仅当x=1∈时，函数g(x)取得最大值．故f(x) = - (x-1)²+，于是当x=2时，f(x)有最小值为．

12．（1）当m=0时，x∈R；当m≠0时，m＞0且△≤0，解得：0＜m≤1，故实数m的取值范围为0≤m≤1．（2）当m=0时，f(0)=；当0＜m≤1时，因，故f(m) = （0＜m≤1）．于是，f(m) = （0≤m≤1），其值域为[0，]．