高三数学第四次阶段测试
数学试卷
时间：120分钟 满分：150分
第I卷(共60分)
| 得分 | 阅卷人 |
|
|
|
1. 选择题(本大题满分60分,每小题5分)本大题共有12小题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的.
1.设集合
，
，则
（
）
A、
B、
C、
D、
2．已知
（ ）
A
B
－
C
D
－
3．函数f(x)=logax(a＞0且a≠1)对任意正实数x,y都有（ ）
A .f(x·y)=f(x)·f(y) B. f(x+y)=f(x)·f(y)
C . f(x·y)=f(x)+f(y) D .f(x+y)=f(x)+f(y)
4.设e1、e2是两个不共线向量,若向量a=3e1+5e2与向量b=me1－3e2共线，则m的值等于 （ ）
A.－
B.－
C.－
D.－
5．下列函数中，既为偶函数又在（0，π）上单调递增的是（ ）
A．
. B．y=cos(－x).
C．y=tgx D．
.
6.一个等差数列共n项，其和为90，这个数列的前10项的和为25，后10项的和为75，则项数n为（ ）
A.14 B.16 C.18 D.20
7．若直线经过点（2，4）且在两坐标轴上的截距的绝对值相等，这样的直线一共有 （ ）
A 1条 B 2条 C 3条 D 4条
8．已知
，下列命题正确的是 （ ）
A．
B．
C．
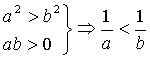D．．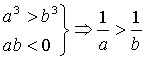
9．(a2-1)x2-(a-1)x-1<0的解集是R,则实数a的取值范围是 （ ）
A.
B. 
C. 
D.A、B、C均不对
10．若点
在直线
上.则
的最小值是 （ ）
A． 
B．8 C．3 D． 
11．设函数f（x）=2－x，函数g（x）的图象与f（x）的图象关于直线y=x对称，函数h（x）的图象由g（x）的图象向右平移1个单位得到，则h（x）为（ ）
A .log2（－x+1） B.－log2（x+1）
C.log2（－x－1） D.－log2（x－1）
12.给出下列四个命题:⑴如果
,那么
⑵函数
在R上是奇函数；
(3) 
的最小值是2
⑷y＝f (x－2)与y＝f (2－x)的图象关于直线x＝2对称
这四个命题中, 错误的命题有（ ）
A.1个 B.2个 C.3个 D.4个
第
卷(共90分)
| 得分 | 阅卷人 |
|
|
|
二．本题满分24分.、填空题：本题共有6小题．只要求直接填写结果，每题填对得4分，否则一律是零分）
13．函数
的定义域为
.
14.设定义在R上的偶函数f(x)满足f(x+1)+f(x)=1,且当x∈［1,2］时，f(x)=2－x,
则f(8.5)=_________.
15.对于任意定义在R上的函数f（x），若存在x0∈R满足f（x0）=x0，则称x0是函数f（x）
的一个不动点。若函数f（x）=x2+ax+1没有不动点，则实数a的取值范围是____________.
16．若某等差数列{an}中，a2+a6+a16为一个确定的常数，则其前n项和Sn中也为确定的常数的是
17．锐角△ABC中，若B=2A，则
的取值范围是___________.
18. 直线 x＋ycosα－1＝0 的倾斜角的取值范围是
| 得分 | 阅卷人 |
|
|
|
三.解答题：本题共有5小题，要求写出解答过程和演算、证明步骤.本题满分66分
19.（本小题满分12分）设二次函数f(x)=x2+x+c(c＞0)，若方程f(x)=0有两个
实数根x1, x2 且x1＜x2.求x2－x1的取值范围；
20．（本小题满分12分）已知平面向量a=(
,－1),b=(
,
),若存在不为零的实
数k和角α,使向量c=a+ (sinα－3)b, d=－ka+(sinα)b,且c⊥d，试求实数k
的取值范围.
21.（本小题满分14分）某村计划建造一个室内面积为800
的矩形蔬菜温室。在温室内，沿左．右两侧与后侧内墙各保留1
宽的通道，沿前侧内墙保留3宽的空地。当矩形温室的边长各为多少时？蔬菜的种植面积最大。最大种植面积是多少？
22.（本小题满分14分）已知函数f（x）=log2（x+m），且f（0）、f（2）、f（6）成等差数列.
（1）求实数m的值；
（2）若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断：
f（a）+f（c）与2f（b）的大小关系，并证明你的结论.
23.（本小题满分14分）已知
（1）若
能表示成一个奇函数
和一个偶函数
的和，求和的解析式；
（2）若和在区间
上都是减函数，求a的取值范围
（3）在（2）的条件下，比较
的大小．