高三数学第一次月考理科卷
数学（理科）试卷
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项符合题目要求.
1．
的虚部为（ ）
A．
B．
C．8
D．
2．设
：
，
：
，则下列命题为真的是（ ）
A．若
则
B．若则 C．若则 D．若则
3．已知
的最大值为2，
的最大值为
，则的取值范围是（ ）
A．
B．
C．
D．以上三种均有可能
4．下列极限中，其值等于2的是（ ）
A．
B．
C．
D．
5．欲对某商场作一简要审计，通过检查发票及销售记录的2%来快速估计每月的销售总额.现采用如下方法：从某本50张的发票存根中随机抽一张，如15号，然后按序往后将65号，115号，165号，…发票上的销售额组成一个调查样本.这种抽取样本的方法是（ ）
A．简单随机抽样 B．系统抽样 C．分层抽样 D．其它方式的抽样
6．若函数
的图象按向量
平移后，它的一条对称轴是
，则
的一个可能的值是（ ）
A．
B．
C．
D．
7．数列
满足
并且
.则数列的第100项为（ ）
A．
B．
C．
D．
8．在长方体
中，
、
分别是棱
、
的中点，若
，则异面直线
与
所成的角为（ ）
A．
B．
C．
D．
9．设
、
为曲线
： 
的焦点，
是曲线
：
与的一个交点，则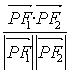
的值为（ ）
A．
B．
C．
D．
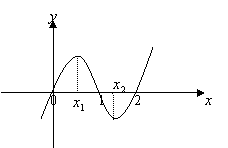10．如图是函数
的大致
图象，则
等于（ ）
A．
B．
C．
D．
11．某人制定了一项旅游计划，从7个旅游城市中选择5个进行游览.如果A、B为必选
城市，并且在游览过程中必须按先A后B的次序经过A、B两城市（A、B两城市可以不
相邻），则有不同的游览线路（ ）
A．120种 B．240种 C．480种 D．600种
12．期中考试以后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M:N为（ ）
A. 
B.
1
C. 
D.
2
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
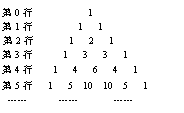13．如图，在由二项式系数所构成的杨辉三角形中，第
_____行中从左至右第14个数与第15个数的比为
.
14．正三棱锥的顶点都在同一个半径为
的球面上，球
心到该棱锥底面的距离是球半径的一半，则该棱锥的体
积是____________________.
15．过点
的直线
将圆：
分成两段弧，当其中的劣弧最短时，直线的方程为 __________
.
16．一水池有2个进水口，1 个出水口，进出水速度如图甲、乙所示. 某天0点到6点，
该水池的蓄水量如图丙所示.（至少打开一个水口）
 |
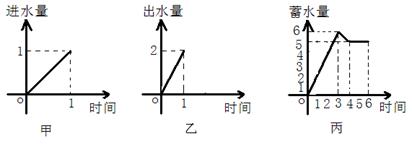给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水.则一定能确定正确的论断序号是_______________.
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
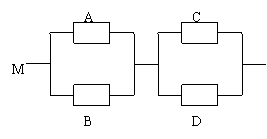17．（本小题满分12分）如图，用
表示四类不同的元件连接成系统.当元件
至少有一个正常工作且元件
至少
有一个正常工作时，系统正常工作.已知
元件正常工作的概率依次为0.5，
0.6，0.7，0.8，求元件连接成的系统正常
工作的概率
.
18．（本小题满分12分）在
中，
分别是
的对边长，已知成等比数列，且
，求
的大小及
的值.
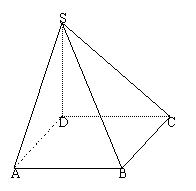19．（本小题满分12分）如图，四棱锥
的底面
是边长为1的正方形，SD垂直于底面ABCD，
.
（1）求证：
；
（2）求平面ASD与平面BSC所成二面角的大小；
（3）设棱SA的中点为M，求异面直线DM与SB所成角
的大小.
20．（本小题满分12分）对于任意实数
，符号
表示
的整数部分，即是不超过的最大整数.在实数轴（箭头向右）上是在点左侧的第一个整数点，当是整数时就是.这个函数叫做“取整函数”也叫高斯（Gauss）函数.
从的定义可得下列性质：
.
与有关的另一个函数是
，它的定义是
，称为的“小数部分”.
（1）根据上文可知，的取值范围是____________，
=_____________；
（2）求
的和.
21．（本小题满分12分）某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元.
（1）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？
（2）设一次订购量为个，零件的实际出厂单价为P元，写出函数
的表达式；
（3）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，利润又是多少元？（工厂售出一个零件的利润＝实际出厂单价－成本）
22．（本小题满分14分）已知 
，
、
为直角坐标平面内、
轴正方向上的单位向量，若向量
=+(+2), 
=+(－2),且
.
（1）求点
的轨迹C的方程；
（2）过点
作直线与曲线C交于A、B两点，设 
，是否存在这样的直线，使得四边形OAPB是矩形？若存在，求出直线的方程；若不存在，请说明理由.
参考答案
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | A | C | B | B | A | D | D | B | C | D | B |
二、填空题：
13．34 14．
或
15．
16．①
三、解答题：
17．解：由A，B构成系统F，由C，D构成系统G，那么系统F正常工作的概率
，系统G正常工作的概率为
，由已知，得
，故系统M正常工作的概率为0.752.
18．解：（1）
成等比数列 
又
，在中，由余弦定理得
（2）在中，由正弦定理得
19．（1）证明：
底面ABCD是正方形 
底面ABCD 
DC是SC在平面ABCD上的射影
由三垂线定理得
（2）解：底面ABCD，且ABCD为正方形
可以把四棱锥补形为长方体
，如图2
面ASD与面BSC所成的二面角就是面
与面
所成的二面角，
又
为所求二面角的平面角
在
中，由勾股定理得
在
中，由勾股定理得
即面ASD与面BSC所成的二面角为
（3）解： 
是等腰直角三角形 又M是斜边SA的中点
面ASD，SA是SB在面ASD上的射影
由三垂线定理得
异面直线DM与SB所成的角为
20．（1）的取值范围是
；
（2）
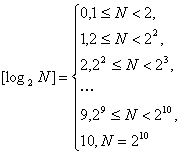
所以，原式=
.
21．解：（1）设每个零件的实际出厂价恰好降为51元时，一次订购量为
个，则
因此，当一次订购量为550个时，每个零件的实际出厂价恰好降为51元.
（2）当
时，
当
时，
当
时，
，所以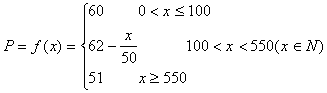
（3）设销售商的一次订购量为x个时，工厂获得的利润为L元，则
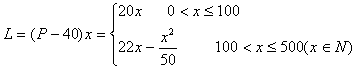
当
时，
；当
时，
因此，当销售商一次订购500个零件时，该厂获得的利润是6000元；如果订购1000个，利润是11000元.
22．解：（1）由题设得
由椭圆定义知，轨迹方程为
4分
（2）∵直线过点（0，3）若直线的斜率不存在，则A、B为椭圆的顶点
∵=
，∴O、P重合与 OAPB是矩形矛盾.
6分
∴直线的斜率存在，设直线的方程为y=kx+3代入，
得（4+3k2）x2+18kx－21=0,则有△=（18k）2－4（4+3k2）（－21）＞0
且
（*）
9分
∵，∴四边形OAPB是平行四边形.
假设存在直线使得四边形OAPB是矩形，则有
，
11分
即有
（1+k2）x1x2+3k(x1+x2)+9=0
将（*）代入，解得k=
均适合△=＞0
13分
∴存在直线:
，使得四边形OAPB是矩形.
14分