高三数学函数测试题
一、选择题（本题每小题5分，共60分）
1.已知集合
，集合
，则
是 ( )
(A) 
(B) 
(C) 
(D) 
2.函数y =2－
(0≤x≤4)的值域是
( )
(A) [－2,2]
(B)[1,2]
(C)[0,2] (D)[－
,]
3.已知函数
，那么
的值为
( )
（A）9
（B）
（C）-9 （D）
4.已知命题“p：
”，命题“q:
,如果“p且q”与“非q”同时为假命题，
则满足条件的
为
（ ）
（A）
（B）
（C）
（D）
5. 函数
上的最大值与最小值的和为3，则a为
（ ）
A．
B．2 C．4 D．
6.设函数
表示除以3的余数,对
都有
( )
(A) 
(B)
(C) 
(D)
7.函数
的图象是
( )
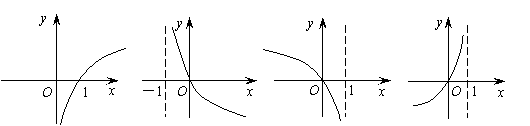(A)
(B)
(C)
(D)
8. 设
分别是定义在R上的奇函数和偶函数，当
时，
且
则不等式
的解集是（ ）
A．
B．
C．
D．
9.要使函数
在［１，２］上存在反函数，则
的取值范围是 ( )
A．≤１ B．≥２ C．≤１或≥２ D．１≤≤２
10.由等式
定义
，则
等于 （ ）
（
）
（
）
（
）
（
）
11. 二次函数
满足
, 又
,
.若在
有最大值3, 最小值1, 则
的取值范围是
（ ）
A．
B．
C．
D．
12. 若方程
有正数解，则实数的取值范围是
（ ）
A．
B．
C．
D．
二、填空题（本题每小题4分，共16分）
13.某公司生产三种型号的轿车,产量分别为1200辆，6000辆和2000辆，为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取______，_______，_______辆．
14. 已知函数
为常数）图象上点A处的切线与
的夹角为
则A点的横坐标为
.
15. 若方程
在∈(0,3)内有唯一解，则实数m的取值范围是
.
16. 设函数
，给出下列4个命题：
①
时，
只有一个实数根； ②
时，
是奇函数；
③的图象关于点
对称；
④方程至多有2个实数根
上述命题中的所有正确命题的序号是 .
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
请把选择题的答案填入下表
答题卷
姓名 得分
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题
13. 14. 15. 16.
三、解答题
17.设函数
(为实数).
(Ⅰ)若<0,用函数单调性定义证明:
在
上是增函数;
(Ⅱ)若=0,
的图象与的图象关于直线
对称,求函数的解析式.
18.已知二次函数
满足：①在
时有极值；②图象过点
，且在该点处切线与直线
平行.
(Ⅰ)求的解析式;
(Ⅱ)求函数
的单调递增区间.
19.已知函数
(
，
为实常数)
(I) 若＝2，b＝－1，求的值域．
(II) 若的值域为[0，＋∞]，求常数，b应满足的条件．
20.甲方是一农场，乙方是一工厂. 由于乙方生产须占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润（元）与年产量t（吨）满足函数关系
.若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格），
(I)将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方获得最大利润的年产量；
(II)甲方每年受乙方生产影响的经济损失金额
（元），在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格s是多少？
21.已知
在=±1时取得极值，且
.
(I)试求常数、、
的值；
(II)试判断=±1是函数的极小值还是极大值，并说明理由.
22. 定义在(-1 ，1)上函数满足
①对任意的
，都有
；②当 
(-1，0)时，有>0.
(I)试判定的奇偶性；
(II)试判定在(-1，0)和(0，1)的单调性；
(Ⅲ)证明：
高三数学函数测试题1参考答案
一、(1)C. (2)C. (3)B. (4)C. (5)B. (6)A. (7)C. (8)B. (9)B. (10)D. (11)D. (12)D.
二、(13)（0，1
. (14)5. (15)f(x)＝
等. (16)19kg.
(19)(I) ∵ x2＋2x－1＝(x－1)2－2≥－2，∴
≥0,
∴ f(x)的值域为[2，+∞]．
(II)当a＝0时，则须x2＋b的最小值≤0，∴b≤0 ;
当a≠0时，只须a＜0，且x2＋ax＋b＝
的最小值
＝a2，
即4b＝5a2. ∴ a＝0，b≤0或a＜0，4b＝5a2 .
(22) (满分14分)
解：⑴令x=y=0，得f(0)=0.再令x=-y，则f(x)+f(-x)=f(0)=0，
∴f(-x)=-f(x) ∴f(x)在(-1 ，1)上为奇函数.
⑵设-1<x1<x2<0，∴(x1+1)(x2-1)<0，∴x1x2-1<x1-x2<0 ，
∴0>
>-1 ∴f()>0，
则f(x1)-f(x2)=f(x1)+f(-x2)=
f()>0 即f(x1)>f(x2).
∴f(x) 在(-1，0)上为单调减函数.∵f(x)为奇函数，∴ f(x)在(0，1)也是减函数.
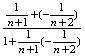⑶∵f(
)=f[
]=f[
]
=f(
)+f(
)=f()-f(
)
∴左边=[f(
)-f(
)]+[f()-f(
)]+…+[ f()+f()]=f()-f()
∵f(x) 为奇函数，又x(-1，0)时，有f(x)>0，∴x(0，1)时，有f(x)<0
∵0<<1，∴f()<0，∴左边> f().