高三数学寒假作业(一)
一、选择题：本大题共计12小题，每小题5分，共60 分
1.设
，集合A＝{xf(x)＝x,x∈R}，B＝{xf[f(x)]＝x,x∈R},则A与B的关系是
（ ）
A．A∩B＝A B．A∩B＝φ C．A∪B＝R D．A∪B＝{－1，0，1}
2．设直线
的倾斜角为
，则该直线关于直线
（
）对称的直线的倾斜角为 （ ）
A.
B. 
C. 
D.
3．过点（1，2）总可以作两条直线与圆x2+y2+kx+2y+k2-15=0相切，则实数k的取值范围（ ）
（A）k>2 （B）-3<k<2 （C）k<-3或k>2 （D）都不对
4．在数列
中，
，
，则
（ ）
A、1
B、
C、
D、
5．△ABC的顶点B在平面a内，A、C在a的同一侧，AB、BC与a所成的角分别是30°和45°,若AB=3,BC=
,AC=5,则AC与a所成的角为
(A)60° (B)45° (C)30° (D)15°
6．已知P为抛物线y2＝4x上任一动点，记点P到y轴的距离为d，对于给定点A(4，5)，则PA＋d的最小值为 （ ）
A.4 B. C.－1 D.－1
7．已知
若
，则
的值为（ ）
A、
B、
C、
D、
( )
9.设函数f（x）=
+x （x∈R）当
时，f（msin）+f（1-m）＞0恒成立，则实数m的范围是：（ ）
（A）（0，1） （B）
（C）
（D）
10．设偶函数f（x）=logax-b在上递增，则f（a+1）与f（b+2）的大小关系是： （ ）
（A）f（a+1）＞f（b+2） （B）f（a+1）≥f（b+2）
（C）f（a+1）＜f（b+2） （D）f（a+1）≤f（b+2）
11.椭圆
的两个焦点为F1和F2，以F1F2为边作正三角形，若椭圆恰好平分正三角形的另两边，则椭圆的离心率为；（ ）
（A）
（B）
（C）
（D）
12.设双曲线
（a>0,b>0）的两个焦点为
、
，点Q为双曲线上除顶点外的任一点，过焦点作∠Q的平分线的垂线，垂足为P，则P点的轨迹为；（ ）
（A）椭圆的一部分 （B）双曲线的一部分
（C）抛物线的一部分 （D）圆的一部分
第Ⅱ卷(非选择题)
二、填空题：本大题共6小题；每小题4分，共24分．
13. 把函数y=2x2-4x+5的图象按向量a平移,得到y=2x2的图象,
且a⊥b,c=(1,-1),b•c=4,则b=___.
14.设曲线y=
与y=x+2有且只有一个公共点P，O为坐标原点，则OP2的取值范围是
。
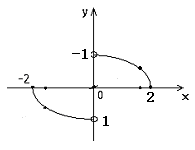
15．如图,函数
的图象是中心在原点,焦点在
轴上的椭圆的两段弧,则不等式
的
解集为 。
16．
是正实数，设
是奇函数}，若对每个实数
，
的元素不超过2个，且有使含2个元素，则的取值范围是 .
（17．在正方形
中，过对角线
的一个平面交
于E，交
于F，则
① 四边形
一定是平行四边形
② 四边形有可能是正方形
③ 四边形在底面ABCD内的投影一定是正方形
④ 四边形有可能垂直于平面
以上结论正确的为 。（写出所有正确结论的编号）
18.方程f（x）=x的根称为函数f（x）的不动点，若函数f（x）= 
有唯一不动点，且x1=1000，xn+1=
（n∈N*），则x2006= 。
三、解答题：本大题共5小题；解答应写出文字说明，证明过程或演算步骤．
19．(本小题满分12分)
已知
（1）求
的值；
（2）求
的最小值．
20（本大题满分12分）
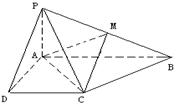已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，
底面ABCD，且PA=AD=DC=AB=1，M是PB的中点。
（Ⅰ）证明：面PAD⊥面PCD；
（Ⅱ）求AC与PB所成的角；
（Ⅲ）求面AMC与面BMC所成二面角的大小。
21．（本小题满分14分）
已知函数
（a，b为常数）且方程f(x)－x+12=0有两个实根为x1=3, x2=4.（1）求函数f(x)的解析式；
（2）设k>1，解关于x的不等式；
.
22．（本小题满分14分）
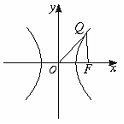
如图，已知△OFQ的面积为2
，且
·
=m，
（1）设<m<4，求向量与的夹角θ的取值范围；
（2）设以O为中心，F为焦点的双曲线经过点Q，=c，
m=（
－1）c2，当
取最小值时，求此双曲线的方程．
23．（本小题满分14分）
如图，直线
相交于点P.直线l1与x轴交于点P1，过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2，过点P2作x轴的垂线交直线l2于点Q2，…，这样一直作下去，可得到一系列点P1、Q1、P2、Q2，…，点Pn（n=1，2，…）的横坐标构成数列
（Ⅰ）证明
；
（Ⅱ）求数列
的通项公式；
（Ⅲ）比较
的大小