高三数学寒假作业

高三数学寒假作业(一)

一、选择题。

1、已知实数满足1<a<2，命题P：函数在区间［0，1］上是减函数；命题：是x<a的充分不必要条件。则__________

A．p或q为真命题　　　　　

B．p且q为假命题

C．非P且q为真命题　　　　

D．非p或非q为真命题

2、已知方程的四个根组成一个首项为的等差数列，则｜m－n｜＝____________

A．1　 　B．　 C．　　D．

3、当时，令为与中的较大者，设a、b分别是f(x)的最大值和最小值，则a＋b等于

A．0　　　 　　B．　　

C．1－　　　D．

4、若直线过圆的圆心，则ab的最大值是

A．　　B．　　C．1　　D．2

5、正四面体的四个顶点都在一个球面上，且正四面体的高为4，则球的表面积为

A．　　 B．18

C．36　 　　D．

6、过抛物线的焦点下的直线的倾斜角，交抛物线于A、B两点，且A在x轴的上方，则｜FA｜的取值范围是(　　　)

A．　　 B．　　　

C．　　　　　D．

二、填空题。

7、若

且a：b＝3：2，则n＝________________

8、定义区间长度m为这样的一个量：m的大小为区间右端点的值减去区间去端点的值，若关于x的不等式，且解的区间长度不超过5个单位长，则a的取值范围是__________

9、已知是不同的直线，是不重合的平面，给出下列命题：

(1)若，则平行于平面内的任意一条直线

(2)若，，，则

(3)若，，，则

(4)若，，则

上面命题中，真命题的序号是__________

(写出所有真命题的序号)

10、已知向量，，令

，求函数的最大值、最小正周期，并写出在［0，］上的单调区间。

11、已知函数

(1)若在区间［1，＋］上是增函数，求实数a的取值范围。

(2)若是的极值点，求在［1，a］上的最大值；

(3)在(2)的条件下，是否存在实数b，使得正数的图象与函数的图象恰有3个交点，若存在，请求出实数b的取值范围；若不存在，试说明理由。

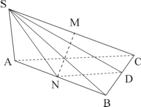
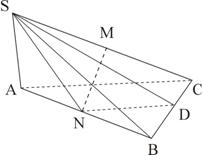12、如图三棱锥S－ABC中，SA平面ABC，，SA＝BC＝2，AB＝4，M、N、D分别是SC、AB、BC的中点。

(1)求证MNAB；

(2)求二面角S－ND－A的正切值；

(3)求A点到平面SND的距离。

高三数学寒假作业(二)

一、选择题。

1、设集合A＝，，则方程表示焦点位于y轴上的椭圆有(　　　)　

A．5个　B．10个　C．20个　D．25个

2、不等式的解集是

A．　　

B．　　

C．

D．

3、的图像关于点对称，且在处函数有最小值，则的一个可能的取值是

A．0　　B．3　　C．6　　D．9

4、五个旅客投宿到三个旅馆，每个旅馆至少住一人，则住法总数有(　)种

A．90　　B．60　　C．150　　D．180

5、不等式成立，则x的范围是

A．　　　　B．　　　
C．　　　　D．

6、的通项公式是，a、

b为正常数，则与的关系是

A．　　B．　

C．　　D．与n的取值有关

二、填空题。

1、正方体的棱长为a，则以其六个面的中心为顶点的多面体的体积是___________

2、的图象是中心对称图形，对称中心是________________

3、对于两个不共线向量、，定义为一个新的向量，满足：

(1) ＝(θ为与的夹角)

(2) 的方向与、所在的平面垂直

在边长为a的正方体ABCD－A′B′C′D′中，()·＝______________

三、解答题。

1、设，是的两个极值点，且

(1)证明：0<a≤1

(2)证明：

(3)若，证明：当且时，

2、双曲线两焦点F₁和F₂，F₁是的焦点，两点,B(1，2)都在双曲线上。

(1)求点F₁的坐标

(2)求点F₂的轨迹

3、非等边三角形ABC外接圆半径为2，最长边BC＝，求的取值范围。

高三数学寒假作业(三)

命题人：周元章

一、选择题。

1、已知点，，动点P满足，当点P的纵坐标是时，点P到坐标原点的距离是

A．　B．　C．　　D．2

2、设A、B、C、D是球面上的四个点，且在同一平面内，AB＝BC＝CD＝DA＝3，球心到该平面的距离是球半径的一半，则球的体积是

A．　　　B．　

C．24　　D．72

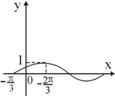
3、若函数的图象(部分)如下图所示，则和的取值是

A．，　　　

B．，

C．，　　　

D．

4、有两排座位，前排11个座位，后排12个座位，现安排2人就座，规定前排中间的3个座位不能坐，并且这2人不左右相邻，那么不同排法的种数是

A．234　B．346　C．350　　D．363

5、已知点、，动点P(x，y)满足·＝x²，则点P的轨迹是

A．圆　　　　　　B．椭圆　　　　

C．双曲线　　　　D．抛物线

6、已知函数，则下列命题正确的是

A．是周期为1的奇函数

B．是周期为2的偶函数

C．是周期为1的非奇非偶函数

D．是周期为2的非奇非偶函数

二、填空题。

7、若经过点P(－1，0)的直线与圆相切，则此直线在y轴上的截距是_____________

8、______________

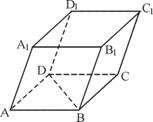9、如图，四棱柱ABCD－A₁B₁C₁D₁的底面ABCD为正方形，侧棱与底面边长均为2a，且，则侧棱AA₁和截面B₁D₁DB的距离是_______________

10、已知四棱锥P－ABCD，底面ABCD是菱形，，PD平面ABCD，PD＝AD，点E为AB中点，点F为PD中点。

(1)证明平面PED平面PAB

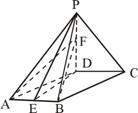(2)求二面角P－AB－F的平面角的余弦值

11、设椭圆方程为，过M(0，1)的直线交椭圆于A、B，O是原点，点P满足，点N的坐标为，当绕点M旋转时，求

(1)动点P的轨迹方程；

(2)的最大值与最小值。

12、已知函数的最大值不大于，又当时，，

(1)求a的值

(2)设，，，证明：

高三数学寒假作业(四)

命题人：王桂林

一、　选择题。

1、函数的图象关于(　　　)

A．x轴对称轴　　B．直线y＝x对称

C．原点对称　　　D．y轴对称

2、双曲线的左焦点为F，点P为左支下半支异于顶点A的任意一点，则直线PF的斜率变化范围是(　　　)

A．(－，0)　　 　　

B．

C．　　

D．

3、设是可导函数，且，则＝(　　)

A．　B．－1　　C．0　　D．－2

4、使点，到直线的距离分别等于1和3，这样的直线有(　　)

A．4条　B．3条　C．2条　D．1条

5、函数的最大值等于(　　)

A．　　　　B．　

C．　　　　D．

6、若函数在x>0上可导，且满足不等式恒成立，又常数a、b满足a>b>0，则下列不等式一定成立的是(　　)

A．

B．

C．

D．

二、填空题。

7、函数的值域_______

8、关于x的不等式的解集为［m，n］，若n－m＝3，则实数k的值为______________

9、设，若满足a＋1且a－1，则称a为孤立元，设的无孤立元的4元子集个数为，则与的关系是__________(写出一个a_n、a_n＋1有关的等式)。

三、解答题

10、某次有奖竞猜活动中，主持人准备了A、B两个互相独立的问题，并宣布，观众答对问题A可获奖金a元，答对问题B可获奖金2a元；先答哪个题由观众自由选择；只有第一个问题答对，才能再答第2个问题，否则中止答题，若你被选为幸运观众，

且假设你答对问题A、B概率分别为，，

你觉得应先回答哪个问题才能使你获得奖金的期望较大？说明理由。

11、矩形ABCD中，，BC＝2，沿对角线BD将向上折起，使A移至P且P在面BCD的射影O落在DC边上。

(1)求证：O是CD的中点

(2)求二面角P－BD－C的大小

(3)求点C到面PBD的距离

2、由原点Ｏ向三次曲线引切线，切于P₁(x₁，y₁)(O、P₁两点不重合)，再由P引此曲线的切线，切于点P₂(x₂，y₂)(P₁P₂不重合)，如此继续下去，得到点列

(1)求x₁

(2)求x_n与x_n＋1满足的关系式。

(3)若a>0，判断x_n与a的大小关系并说明理由。

高三数学寒假作业(五)

命题人：陈翠菊

一、选择题。

1、已知集合，，若只有一个子集，则k的取值范围是(　　　)

A．　　B．　　　

C．　　D．

2、设双曲线

的一条准线与两条渐近线交于A、B两点，相应的焦点为F，若以AB为直径的圆过F点，则双曲线的离心率为(　　　)

A．　　B．　C．2　　D．

3、箱子里有5个黑球，4个白球，每次随机取出一个球，若取出是黑球，则放回箱中，重新取球；若取出白球，则停止取球，那么第4次取球即停止的概率为(　　　)

A．　　　B．　　　　

C．　　　D．

4、(理)复数满足，则的最小值为(　)

A．2　B．4　　C．　D．

　　(文)设，且，则(　　　)

A．　　B．

C．　 D．

5、(理)函数，在

上的最大值点为(　　　)

A．0　　　B．　　C．　　D．

(文)函数有(　　)

A． 一个极大值和一个极小值　

　　B．两个极大值和一个极小值

C．一个极大值和两个极小值　　　　

D．两个极大值和两个极小值

6、设方程和方程的两根分别是p、q，函数，则

A．

B．

C．　　　　　　　

D．

二、填空题。

7、设二项式的展开式中，

各项的系数和M，所有二项式系数的和为N，如果M＋N＝272，则n＝______________

8、设直线与抛物线相交于A、B两点，O为坐标原点，若，则与轴交点的横坐标的取值范围是____________

9、设，且＝1，则对任何实数a、b、x，f(x)的最大值的取值范围是_________________

10、(本题满分12分)现有甲、乙、丙三人独立参加入学考试，合格的概率分别为，求：

(1)三人中至少有一人合格的概率；

(2)三人中有两人合格的概率；

(3)合格人数的数学期望。

11、(本题满分12分)若为双曲

线的左右焦点，0为坐标原点，

P在双曲线的左支上，点M在右准线上，且

满足；，

(1)求该双曲线的离心率；

(2)若该双曲线过，求双曲线的方程；

(3)若过的双曲线的虚轴端点分别为、(B₁在y轴正半轴上)，点A、B在双曲线上，且，求时，直线AB的方程。

12、(本题满分12分)已知函数在区间［0，1］上单调递增，在区间［1，2］上单调递减；

(1)求a的值；

(2)求证：x＝1是该函数的一条对称轴

(3)是否存在实数b，使函数的图象与函数f(x)的图象恰好有两个交点？若存在，求出b的值；若不存在，请说明理由。

高三数学寒假作业(六)

一、选择题。

1、已知抛物线上一定点A(－1，0)和两定点P、Q，当PAPQ时，点Q的横坐标的取值范围是(　　　)

A．　　B．　　　

C．　　　D．

2、四面体的顶点和各棱中点共有10个点，在其中取4个不共面的点，不同的取法共有(　　　)

A．150种　　　B．147种　

C．144种　　　D．141种

3、如果函数的定义域是，则的定义域(　　)

A．［1，2］　　　B．［1，5］　

C．［1，17］　　　D．［5，17］

4、在－6，－4，－2，0，1，3，5，7这8个数中，任取两个不同的数分别作为虚数a＋b的实部和虚部，则所能组成的所有不同虚数中，模大于5的虚数的个数是(　)

A．32　　B．34　　C．42　　D．43

5、若

的最小正周期是1，则实数t的值为(　　　)　　

A．1　　B．±1　C．　　D．±

6、与双曲线有共同渐近线，且经过点的双曲线的一个焦点到一条渐近线的距离是(　　)

A．　　　　B．　

C．　　　　D．1

7、函数对于x<0时，总有，则a的取值范围是________

8、要排一个有6个独唱节目和4个合唱节目的演出表，如果合唱的节目不排头，并且任何2个合唱节目不相邻，则不同的排法种数是____________

9、求函数的值域。

10、已知函数

(1)求f(x)的定义域和值域；

(2)判断它的奇偶性

(3)求出它的单调区间；

(4)判断它的周期。

11、如图所示，已知G是ABO的重心。

(1)求；

(2)若PQ过ABO的重心G，且，，，，求证：

12、已知数列和，有，，而的前n项和

(1)求b_n

(2)用n表示，并求a_n