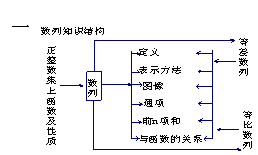
 二、高三数学基本知识点:数列
二、高三数学基本知识点:数列
1![]() 数列是特殊的函数,有些题目可结合函数知识去解决,体现了函数思想、数形结合的思想
数列是特殊的函数,有些题目可结合函数知识去解决,体现了函数思想、数形结合的思想![]()
2![]() 等差、等比数列中,a
等差、等比数列中,a![]() 、
、![]() 、n、d(q)、
、n、d(q)、![]() “知三求二”,体现了方程(组)的思想、整体思想,有时用到换元法
“知三求二”,体现了方程(组)的思想、整体思想,有时用到换元法![]()
3![]() 求等比数列的前n项和时要考虑公比是否等于1,公比是字母时要进行讨论,体现了分类讨论的思想
求等比数列的前n项和时要考虑公比是否等于1,公比是字母时要进行讨论,体现了分类讨论的思想![]()
4![]() 数列求和的基本方法有:公式法,倒序相加法,错位相减法,拆项法,裂项法,累加法,等价转化等
数列求和的基本方法有:公式法,倒序相加法,错位相减法,拆项法,裂项法,累加法,等价转化等![]()
等差数列相关公式:(1)![]() ;(2)通项公式:
;(2)通项公式:![]() ;
;
(3)前n项和公式:![]() ;(4)通项公式推广:
;(4)通项公式推广:![]()
![]()
等差数列![]() 的一些性质:(1)对于任意正整数n,都有
的一些性质:(1)对于任意正整数n,都有![]() ;(2)
;(2)![]() 的通项公式
的通项公式![]() ;(3)对于任意的整数
;(3)对于任意的整数![]() ,如果
,如果![]() ,那么
,那么![]() ;(4)对于任意的正整数
;(4)对于任意的正整数![]() ,如果
,如果![]() ,则
,则![]() ;(5)对于任意的正整数n>1,有
;(5)对于任意的正整数n>1,有![]() ;(6)对于任意的非零实数b,数列
;(6)对于任意的非零实数b,数列![]() 是等差数列,则
是等差数列,则![]() 是等差数列(7)已知
是等差数列(7)已知![]() 是等差数列,则
是等差数列,则![]() 也是等差数列(8)
也是等差数列(8)![]() 等都是等差数列;(9)
等都是等差数列;(9)![]() 是等差数列
是等差数列![]() 的前n项和,则
的前n项和,则![]() 仍成等差数列,即
仍成等差数列,即![]() ;(10)若
;(10)若![]() ,则
,则![]() (11)若
(11)若![]() ,则
,则![]() (12)
(12)![]() ,反之也成立
,反之也成立![]()
等比数列相关公式:(1)定义:![]() ;(2)通项公式:
;(2)通项公式:![]()
![]()
(3)前n项和公式: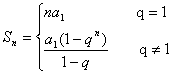 ;(4)通项公式推广:
;(4)通项公式推广:![]()
![]()
等比数列![]() 的一些性质:(1)对于任意的正整数n,均有
的一些性质:(1)对于任意的正整数n,均有![]() ;(2)对于任意的正整数
;(2)对于任意的正整数![]() ,如果
,如果![]() ,则
,则![]() ;(3)对于任意的正整数
;(3)对于任意的正整数![]() ,如果
,如果![]() ,则
,则![]() (4)对于任意的正整数n>1,有
(4)对于任意的正整数n>1,有![]() ;(5)对于任意的非零实数b,
;(5)对于任意的非零实数b,![]() 也是等比数列;
也是等比数列;
(6)已知![]() 是等比数列,则
是等比数列,则![]() 也是等比数列;(7)如果
也是等比数列;(7)如果![]() ,则
,则![]() 是等差数列;
是等差数列;
(8)数列![]() 是等差数列,则
是等差数列,则![]() 是等比数列;(9)
是等比数列;(9)![]() 等都是等比数列;(10)
等都是等比数列;(10)![]() 是等比数列
是等比数列![]() 的前n项和,①当q=-1且k为偶数时,
的前n项和,①当q=-1且k为偶数时,![]() 不是等比数列.②当q≠-1或k为奇数时,
不是等比数列.②当q≠-1或k为奇数时,![]() 仍成等比数列
仍成等比数列![]()
数列前n项和公式:![]() ;
;![]() ;
;
![]() ;等差数列中,
;等差数列中,![]() ;等比数列中,
;等比数列中,![]() ;裂项求和:
;裂项求和:![]() ;(
;(![]() )
)![]()
三、巩固练习(2004年高考试题)
浙江文理(3) 已知等差数列![]() 的公差为2,若
的公差为2,若![]() 成等比数列, 则
成等比数列, 则![]() =(A) –4 (B) –6 (C) –8 (D) –10
=(A) –4 (B) –6 (C) –8 (D) –10
全国卷四文理6.等差数列![]() 中,
中,![]() ,则此数列前20项和等于 A.160 B.180 C.200 D.220
,则此数列前20项和等于 A.160 B.180 C.200 D.220![]()
天津卷理8. 已知数列![]() ,那么“对任意的
,那么“对任意的![]() ,点
,点![]() 都在直线
都在直线![]() 上”是“
上”是“![]() 为等差数列”的A. 必要而不充分条件B. 充分而不必要条件C. 充要条件D. 既不充分也不必要条件
为等差数列”的A. 必要而不充分条件B. 充分而不必要条件C. 充要条件D. 既不充分也不必要条件![]()
全国卷四文18.已知数列{![]() }为等比数列,
}为等比数列,![]() (Ⅰ)求数列{
(Ⅰ)求数列{![]() }的通项公式;
}的通项公式;
(Ⅱ)设![]() 是数列{
是数列{![]() }的前
}的前![]() 项和,证明
项和,证明![]()
![]()
解:(I)设等比数列{an}的公比为q,则a2=a1q,
a5=a1q4. 依题意,得方程组a1q=6, a1q4=162.解此方程组,得a1=2, q=3.故数列{an}的通项公式为an=2·3n-1![]()
(II) ![]()
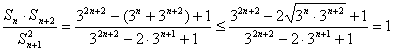
![]()
全国三文(4)等比数列![]() 中
中![]()
![]() ,则
,则![]() 的前4项和为A. 81 B. 120
C. D. 192
的前4项和为A. 81 B. 120
C. D. 192![]()
全国三文⒆设公差不为零的等差数列{an},Sn是数列{an}的前n项和,且![]() ,
,![]() ,求数列{an}的通项公式.
,求数列{an}的通项公式.
解:设数列{an}的公差为d(d≠0),首项为a1,由已知得: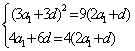 .解之得:
.解之得:![]() ,
,![]() 或
或 ![]() (舍)
(舍)![]()
![]()
全国卷三理⑶设数列![]() 是等差数列,
是等差数列,![]()
![]() ,Sn是数列
,Sn是数列![]() 的前n项和,则( )
的前n项和,则( )
A.S4<S5 B.S4=S5 C.S6<S5 D.S6=S5![]()
全国卷三理(22)已知数列{an}的前n项和Sn满足:Sn=2an +(-1)n,n≥1.⑴写出求数列{an}的前3项a1,a2,a3;
⑵求数列{an}的通项公式;⑶证明:对任意的整数m>4,有![]()
![]()
解:⑴当n=1时,有:S1=a1=2a1+(-1)![]() a1=1;当n=2时,有:S2=a1+a2=2a2+(-1)2
a1=1;当n=2时,有:S2=a1+a2=2a2+(-1)2![]() a2=0;
a2=0;
当n=3时,有:S3=a1+a2+a3=2a3+(-1)3![]() a3=2;综上可知a1=1,a2=0,a3=2;
a3=2;综上可知a1=1,a2=0,a3=2;
⑵由已知得:![]() ,化简得:
,化简得:![]()
上式可化为:![]() ,故数列{
,故数列{![]() }是以
}是以![]() 为首项, 公比为2的等比数列.故
为首项, 公比为2的等比数列.故![]() ∴
∴![]()
![]()
数列{![]() }的通项公式为:
}的通项公式为:![]()
![]()
⑶由已知得:![]()
![]()
![]()
![]()
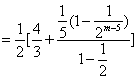
![]()
![]()
![]() . 故
. 故![]() ,( m>4)
,( m>4) ![]()
天津卷文20.
设![]() 是一个公差为
是一个公差为![]() 的等差数列,它的前10项和
的等差数列,它的前10项和![]() 且
且![]() ,
,![]() ,
,![]() 成等比数列。(1)证明
成等比数列。(1)证明![]() ;(2)求公差
;(2)求公差![]() 的值和数列
的值和数列![]() 的通项公式
的通项公式![]()
证明:因![]() ,
,![]() ,
,![]() 成等比数列,故
成等比数列,故![]() ,而
,而![]() 是等差数列,有
是等差数列,有![]() ,
,![]()
于是 ![]()
![]() ,即
,即![]() ,化简得
,化简得 ![]()
![]()
(2)解:由条件![]() 和
和![]() ,得到
,得到![]() ,由(1),
,由(1),![]() ,代入上式得
,代入上式得![]() ,故
,故 ![]() ,
,![]() ,
,![]()
![]()
浙江卷文(17)已知数列![]() 的前n项和为
的前n项和为![]() (Ⅰ)求
(Ⅰ)求![]() ;(Ⅱ)求证数列
;(Ⅱ)求证数列![]() 是等比数列
是等比数列![]()
解: (Ⅰ)由![]() ,得
,得![]() ,∴
,∴![]()
![]() ,又
,又![]() ,即
,即![]() ,得
,得![]() .(Ⅱ)当n>1时,
.(Ⅱ)当n>1时,![]() 得
得![]() 所以
所以![]() 是首项
是首项![]() ,公比为
,公比为![]() 的等比数列
的等比数列![]()
广东卷17. 已知![]() 成公比为2的等比数列(
成公比为2的等比数列(![]() 也成等比数列. 求
也成等比数列. 求![]() 的值
的值![]()
解:∵α,β,γ成公比为2的等比数列,∴β=2α,γ=4α,∵sinα,sinβ,sinγ成等比数列
![]()
![]()
![]()
![]() 当cosα=1时,sinα=0,与等比数列的首项不为零,故cosα=1应舍去,
当cosα=1时,sinα=0,与等比数列的首项不为零,故cosα=1应舍去,![]()
![]()
![]()
北京文理(14)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为5,那么
,公和为5,那么![]() 的值为___,且(文:这个数列的前21项和
的值为___,且(文:这个数列的前21项和![]() 的值为_____)(理:这个数列的前n项和
的值为_____)(理:这个数列的前n项和![]() 的计算公式为__( 3 ;(文:52)理:当n为偶数时,
的计算公式为__( 3 ;(文:52)理:当n为偶数时, ![]() ;当n为奇数时,
;当n为奇数时,![]() )
)
湖北卷理8文9.已知数列{![]() }的前n项和
}的前n项和![]() 其中a、b是非零常数,则存在数列{
其中a、b是非零常数,则存在数列{![]() }、{
}、{![]() }使得( )A.
}使得( )A.![]() 为等差数列,{
为等差数列,{![]() }为等比数列 B.
}为等比数列 B.![]() 和{
和{![]() }都为等差数列 C.
}都为等差数列 C.![]() 为等差数列,{
为等差数列,{![]() }都为等比数列 D.
}都为等比数列 D.![]() 和{
和{![]() }都为等比数列
}都为等比数列![]()
湖南文20.
已知数列{an}是首项为a且公比q不等于1的等比数列,Sn是其前n项的和,a1,2a7,3a4
成等差数列.(I)证明 12S3,S6,S12-S6成等比数列;(II)求和Tn=a1+2a4+3a7+…+na3n ![]()
(Ⅰ)证明 由![]() 成等差数列, 得
成等差数列, 得![]() ,即
,即 ![]() 变形得
变形得 ![]() 所以
所以![]() (舍去).由
(舍去).由 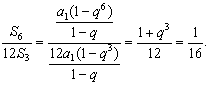
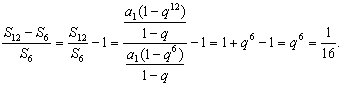 得
得 ![]()
所以12S3,S6,S12-S6成等比数列![]()
(Ⅱ)解:![]()
即 ![]() ①
①
①×![]() 得:
得: ![]()
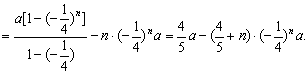 所以
所以 ![]()
江苏卷15.设数列{an}的前n项和为Sn,Sn=![]() (对于所有n≥1),且a4=54,则a1的数值是__2
(对于所有n≥1),且a4=54,则a1的数值是__2![]()
江苏卷20.设无穷等差数列{an}的前n项和为Sn.(Ⅰ)若首项![]() ,公差
,公差![]() ,求满足
,求满足![]() 的正整数k;(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有
的正整数k;(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有![]() 成立
成立![]()
解:(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]()
![]()
上海卷理12
若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号)①S1与S2; ②a2与S3; ③a1与an; ④q与an.其中n为大于1的整数, Sn为{an}的前n项和.(①、④)![]()
全国卷一理15.已知数列{an},满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则{an}的通项
![]()
![]() ( 答案
( 答案![]() )
)![]()
全国卷一理22.已知数列![]() ,且a2k=a2k-1+(-1)k, a2k+1=a2k+3k,
其中k=1,2,3,…….
,且a2k=a2k-1+(-1)k, a2k+1=a2k+3k,
其中k=1,2,3,…….
(I)求a3, a5;(II)求{ an}的通项公式![]()
解:(I)a2=a1+(-1)1=0,a3=a2+31=3. a4=a3+(-1)2=4, a5=a4+32=13, 所以,a3=3,a5=13.
(II) a2k+1=a2k+3k = a2k-1+(-1)k+3k, 所以a2k+1-a2k-1=3k+(-1)k, 同理a2k-1-a2k-3=3k-1+(-1)k-1,
……a3-a1=3+(-1).
所以(a2k+1-a2k-1)+(a2k-1-a2k-3)+…+(a3-a1)=(3k+3k-1+…+3)+[(-1)k+(-1)k-1+…+(-1)],
由此得a2k+1-a1=![]() (3k-1)+
(3k-1)+![]() [(-1)k-1],于是a2k+1=
[(-1)k-1],于是a2k+1=![]()
a2k= a2k-1+(-1)k=![]() (-1)k-1-1+(-1)k=
(-1)k-1-1+(-1)k=![]() (-1)k=1
(-1)k=1 ![]()
{an}的通项公式为: 当n为奇数时,an=![]() 当n为偶数时,
当n为偶数时,![]()
全国卷一文17. 等差数列{![]() }的前n项和记为Sn.已知
}的前n项和记为Sn.已知![]()
![]()
(Ⅰ)求通项![]() ;(Ⅱ)若Sn=242,求n
;(Ⅱ)若Sn=242,求n ![]()
解:(Ⅰ)由![]() 得方程组
得方程组 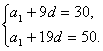 解得
解得![]()
所以 ![]() (Ⅱ)由
(Ⅱ)由![]() 得方程
得方程![]()
![]()
解得![]()
![]()
全国卷二理(19)数列{an}的前n项和记为Sn,已知a1=1,an+1=![]() Sn(n=1,2,3,…)
Sn(n=1,2,3,…)![]()
证明:(Ⅰ)数列{![]() }是等比数列;(Ⅱ)Sn+1=4an
}是等比数列;(Ⅱ)Sn+1=4an ![]()
证(I)由a1=1,an+1=![]() Sn(n=1,2,3,…),知a2=
Sn(n=1,2,3,…),知a2=![]() S1=3a1,
S1=3a1,![]() ,
, ![]() ,∴
,∴![]()
又an+1=Sn+1-Sn(n=1,2,3,…),则Sn+1-Sn=![]() Sn(n=1,2,3,…),∴nSn+1=2(n+1)Sn,
Sn(n=1,2,3,…),∴nSn+1=2(n+1)Sn,
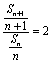 (n=1,2,3,…).故数列{
(n=1,2,3,…).故数列{![]() }是首项为1,公比为2的等比数列
}是首项为1,公比为2的等比数列 ![]()
证(II) 由(I)知,![]() ,于是Sn+1=4(n+1)·
,于是Sn+1=4(n+1)·![]() =4an(n
=4an(n![]() )
)
又a2=3S1=3,则S2=a1+a2=4=4a1,因此对于任意正整数n≥1都有Sn+1=4an ![]()
全国卷二文(17)已知等差数列{an},a2=9,a5 =21 ![]()
(Ⅰ)求{an}的通项公式;(Ⅱ)令bn=![]() ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn ![]()
解:a5-a2=3d,d=4,an=a2+(n-2)d=9+4(n-2)=4n+1;{bn}是首项为32公比为16的等比数列,Sn=![]() .
.
重庆卷理9. 若数列![]() 是等差数列,首项
是等差数列,首项![]() ,则使前n项和
,则使前n项和![]() 成立的最大自然数n是:( ) A 4005 B 4006
C 4007 D
4008
成立的最大自然数n是:( ) A 4005 B 4006
C 4007 D
4008 ![]()
重庆卷理22. 设数列![]() 满足
满足![]() (1) 证明
(1) 证明![]() 对一切正整数n 成立;(2)令
对一切正整数n 成立;(2)令![]() ,判断
,判断![]() 的大小,并说明理由
的大小,并说明理由 ![]()
证(1):由递推公式得
![]()
![]()
上述各式相加并化简得 ![]()
![]()
![]()
![]()
![]()
解(II):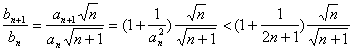
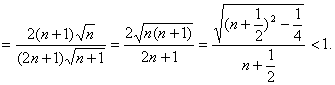
![]()
![]()