高三数学基础题汇编（1）
1 函数
的定义域是
，则函数
的定义域是 ．
2 求函数
的反函数．
3 求
的最小值．
4 设二次函数满足
且
的两实根平方和为
，图象过点
，求
的解析式．
5函数
的定义域为
，则实数
的取值范围是
6 已知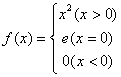
，则
的值是
．
7 设函数
的图象关于直线
对称，若
时，
，则当
时，
．
8 已知是定义在
上的偶函数，且它在
上单调递增，那么使
的实数的取值范围是
．
9 求函数
的单调区间及其增减性 .
10 如果奇函数在区间
上是增函数且最小值为
，那么在区间
上是
(增、减函数)且最 值为
．
11 若
是偶函数，则的单调递增区间是 ．
12 把函数
的图象向右平移1个单位，得到函数的图象，则
．
13 直线
与函数
的图象有两个不同的交点，则
的范围是 ．
14 抛物线
与
轴的两个交点都在点
的右方，则
的取值范围是
．
15 在区间
上，函数
与
在同一点取得相同的最小值，那么在上的最大值是
．
16 若定义在区间
内的函数
满足
，则的取值范围是
．
17 函数
的值域是
．
18 函数
在
上恒有
，则的取值范围是
．
19 已知
在
上是的减函数，则的取值范围是
．
20 如果
，那么、间的关系是
．
21 设是
上的奇函数，
，当
时，
，则
等于
．
22 设函数定义在实数集上，则函数
与
的图象关于（ ）
A 直线
对称 B 直线
对称
C 直线
对称
D 直线对称
23 将
的图象（ ）
A 先向左平行移动1个单位 B 先向右平行移动1个单位
C 先向上平行移动1个单位 D 先向下平行移动1个单位
再作关于直线
对称的图象，可得到函数
的图象．
24 若
，则函数
的图象不经过第 象限．
25 定义在全体实数上的奇函数
要使
，的取值范围是
26 设
，则
．