高三数学冲刺练习（11）

高三数学冲刺练习（11）

1．设P、Q是两个非空集合，定义P*Q=，若P=　　 Q=，则P*Q中元素的个数是 A．4个　B．7个　 C．12个 D．16个

2．过抛物线y²=4x的焦点F作垂直于x轴的直线，交抛物线于A、B两点，则以F为圆心，AB为直径的圆方程是

A．(x－1)²+y²=1 B．(x－1)²+y²=2  C．(x－)²+y²=4 D．(x－1)²+y²=4

3．已知m，是异面直线，给出下列四个命题：①必存在平面，过m且与都平行；②必存在平面 ，过m且与垂直；③必存在平面r，与m，都垂直；④必存在平面w, 与m，的距离都相等。其中正确的结论是

A．①②　　　　  B．①③　　　　  C．②③　　　 D．①④

4．要得到函数y=sin2x的图象，可以把函数y=sin(2x－)的图象

A．向左平移 个单位　　　　　　 B．向右平移个单位　　

C．向左平移 个单位　　　　 　　 D．向右平移 个单位

5.已知真命题：“a≥bc>d”和“a<b”,那么“c≤d”是“e≤f”

A充分不必要条件 B必要不充分条件 C充要条件 D既不充分又必要条件

6．（1）从8盆不同的鲜花中选出4盆摆成一排，其中甲、乙两盆有且仅有一盆展出的不同摆法种数为　　A．1320　B．960　C．600　D．360

（2）从8盒不同的鲜花中选出4盆摆成一排，其中甲、乙两盆不同时展出的摆法种数为　　　A．1320　　  B．960　　　C．600　　D．360

7．设函数f(x)是定义在R上的以3为周期的奇函数，若f(1)>1，f(2)= ，则　A.a<　 B.a<　C.a>　D.－1<a<

8．已知log, 0<a<1，则x₁,x₂,x₃的大小关系是

A．x₃<x_2< x₁  B．x₂<x_1< x₃ 　　　C．x₁<x_3< x₂ 　　　 D．x₂<x_3< x₁

9．（1）已知直线y=kx+1与曲线y=x³+ax+b切于点(1，3)，则b的值为

A．3　　　　  B．－3　　　　　　 C．5　　　　　  D．－5

（2）设曲线y=和曲线y=在它们交点处的两切线的夹角为，则tan为　　　A．1　　　　 B．　　　　  C．　　　　　 D．

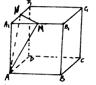10．如图，在棱长为3的正方体ABCD－A₁B₁C₁D₁中，M、N分别是棱A₁B₁、A₁D₁的中点，则点B到平面AMN的距离为

A．　　　　　 B.　　　 C.　　　　　　　D.2　

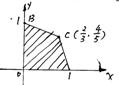11．如图，目标函数u =ax－y的可行域为四边形的OACB（含边界），若()是该目标函数的最优解，则a的取值范围是

A.　　 B.　C.　　 D.　

12．已知为锐角，sin,cos=y, cos()=－,则y与x的函数关系式为

A.y=－　　　　 B.y=－

C.y=－　　　　D. y=－

题号	1	2	3	4	5	6		7	8	9		10	11	12
答案

13．设f(x)= x⁵－5x⁴+10x³－10x²+5x+1，则f(x)的反函数为 f^－1(x)=　　　 。

14.某校有高中生1200人，初中生900人，老师120人，现用分层抽样的方法从所有师生中抽取一个容量为N的样本；已知从初中生中抽取人数为60人，那么N=　　　　　　  。

15．在平面几何中有：Rt△ABC的直角边分别为a,b，斜边上的高为h，则。类比这一结论，在三棱锥P—ABC中，PA、PB、PC两点互相垂直，且PA=a，PB=b，PC=c，此三棱锥P—ABC的高为h，则结论为　　　　　　　 。

16．某大楼共有20层，有19人在第一层上了电梯，他们分别要去第2层至第20层，每层1人，而电梯只允许停 1次，可只使1人满意，其余18人都要步行上楼或下楼，假设乘客有向下走1层的不满意度为1，每向上走一层的不满意度为2，所有人的不满意度之和为S，为使S最小，电梯应当停在第　　　　 层。