高三数学第二学期导师制（03）
班级 姓名 学号 得分
一、填空题：
1．某校高一、高二、高三三个年级的学生数分别为1500人、1200和1000人，现采用按年级分层抽样法了解学生的视力状况，已知在高一年级抽查了75人，则这次调查三个年级共抽查了 人.
2．若
的展开式第二项的值大于1000，则实数x的取值范围为
。
3．下列判断错误的个数为 。
（1）．命题“若q则p”与命题“若
则
”互为逆否命题。
（2）．“am2＜bm2”是“a＜b”的充要条件。
（3）．“矩形的两条对角线相等”的否命题为假。
（4）．命题“
”为真（其中
为空集）。
4．
的值为
.
5．抛物线
与直线
交于两点A、B，其中点A的坐标是（1，2）。设抛物线的焦点为F，则FA+FB等于 。
6．正方形ABCD中，E、分别是AB、CD的中点，沿EF将正方形折成60°的二面角，则异面直线BF与DE所成角余弦值是__ ___。
7．设函数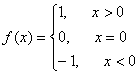
，则方程
的解为 .
8．把120个相同的小球紧密地垒成一个正三棱锥，那么最低一层有 个小球.
9．．函数
的图象的相邻两支截直线
所得线段长为
的值是 。
10．设
上的奇函数，且在区间（0，
）上单调递增，若
，三角形的内角满足
，则A的取值范围是
。
11．函数
取最大值时x的值为
。
12．将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点（-2，4）重合，若点（7，3）与点（m ,n）重合，则m+n的值为 。
二、选择题
13. 若某等差数列{an}中，a2+a6+a16为一个确定的常数，则其前n项和Sn中也为
确定的常数的是 （ ）
A．S17 B．S15 C．S8 D．S7
14．某商场开展促销奖活动，摇奖器摇出的一组中奖号码是6，5，2，9，0，4。参加
抽奖的每位顾客从0，1…，9这十个号码中抽出六个组成一组。如果顾客抽出的
方个号码中至少有5个与摇奖器摇出的号码相同（不计顺序）就可以得奖，某位
顾客可能获奖的概率为 （ ）
（A）
（B）
（C）
（D）
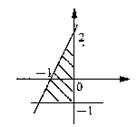
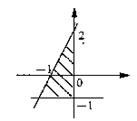
15．方程
所表示的曲线图形是 （ ）
|
|
（16题图）
15．
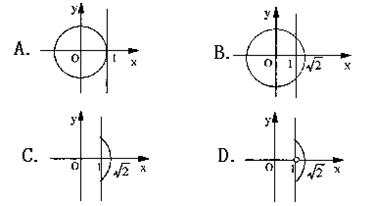
16．上图中阴影部分可用哪一组二元一次不等式表示 （ ）
A．
B．
C．
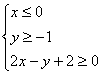D．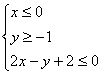
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.
17．已知函数
（Ⅰ）将f(x)写成
的形式，并求其图象对称中心的横坐标；
（Ⅱ）如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为x，试求x的范围及此时函数f(x)的值域.
解：
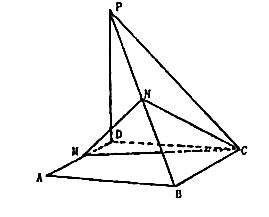18.已知ABCD是矩形，PD⊥平面ABCD，PD=DC=a，
，M、N分别是AD、PB的中点。
（Ⅰ）求证：平面MNC⊥平面PBC；
（Ⅱ）求点A到平面MNC的距离。
解：
20．设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3, 且数列{an+1－an }（n∈N*）是等差数列，数列{bn－2}(n∈N*)是等比数列.
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）是否存在k∈N*，使ak－bk∈（0，
）？若存在，求出k；若不存在，说明理由.
解：
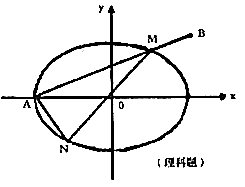20.已知椭圆
，直线l过点A（-a,0）和点B（a,ta）（t>0）交椭圆于M。直线MO交椭圆于N。
（Ⅰ）用a,t表示
的面积S；
（Ⅱ）若
，a为定值，求S的最大值。
解:
高三第二学期 导师制（03）解答
一、填空题：
1．某校高一、高二、高三三个年级的学生数分别为1500人、1200和1000人，现采用按年级分层抽样法了解学生的视力状况，已知在高一年级抽查了75人，则这次调查三个年级共抽查了 185 人.
2．若的展开式第二项的值大于1000，则实数x的取值范围为 x ＞10 。
3．下列判断错误的个数为 1 。
（1）．命题“若q则p”与命题“若则”互为逆否命题。
（2）．“am2＜bm2”是“a＜b”的充要条件。
（3）．“矩形的两条对角线相等”的否命题为假。
（4）．命题“”为真（其中为空集）。
4．的值为 223 .
5．抛物线与直线交于两点A、B，其中点A的坐标是（1，2）。设抛物线的焦点为F，则FA+FB等于 7 。
6．正方形ABCD中，E、分别是AB、CD的中点，沿EF将正方形折成60°的二面角，则异面直线BF与DE所成角余弦值是___ 
___。
7．设函数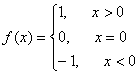，则方程的解为 x=0，2或－
.
8．把120个相同的小球紧密地垒成一个正三棱锥，那么最低一层有 36 个小球.
9．．函数的图象的相邻两支截直线所得线段长为
的值是 0 。
10．设上的奇函数，且在区间（0，）上单调递增，若，三角形的内角满足，则A的取值范围是
。
11．函数取最大值时x的值为
。
12．将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点（-2，4）重合，若点（7，3）与点（m ,n）重合，则m+n的值为 10 。
二、选择题
13. 若某等差数列{an}中，a2+a6+a16为一个确定的常数，则其前n项和Sn中也为
确定的常数的是 （ B ）
A．S17 B．S15 C．S8 D．S7
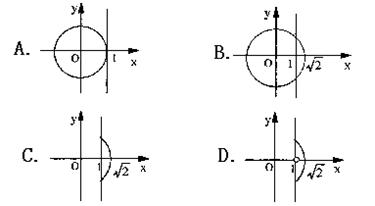
14．方程所表示的曲线图形是 （ D ）
|
15．某商场开展促销奖活动，摇奖器摇出的一组中奖号码是6，5，2，9，0，4。参加
抽奖的每位顾客从0，1…，9这十个号码中抽出六个组成一组。如果顾客抽出的
方个号码中至少有5个与摇奖器摇出的号码相同（不计顺序）就可以得奖，某位
顾客可能获奖的概率为 （ D ）
（A）
（B）
（C）
（D）
16．
|
A． B．
C． D．
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.
17．已知函数
（Ⅰ）将f(x)写成的形式，并求其图象对称中心的横坐标；
（Ⅱ）如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为x，试求x的范围及此时函数f(x)的值域.
解：（Ⅰ）
…3分
由
=0即
即对称中心的横坐标为
…………6分
（Ⅱ）由已知b2=ac
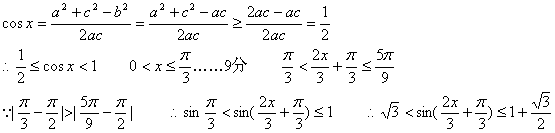即
的值域为
综上所述，
值域为 …………12分
18.已知ABCD是矩形，PD⊥平面ABCD，PD=DC=a，，M、N分别是AD、PB的中点。
（Ⅰ）求证：平面MNC⊥平面PBC；
（Ⅱ）求点A到平面MNC的距离。
解：（I）连PM、MB ∵PD⊥平面ABCD
∴PD⊥MD…1分
∴PM=BM 又PN=NB ∴MN⊥PB………3分
得NC⊥PB∴PB⊥平面MNC……5分
平面PBC
∴平面MNC⊥平面PBC……6分
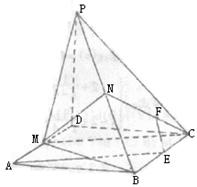（II）取BC中点E，连AE，则AE//MC∴AE//平面MNC，
A点与E点到平面MNC的距离相等…7分
取NC中点F，连EF，则EF平行且等于BN
∵BN⊥平面MNC ∴EF⊥平面MNC，EF长为E
点到平面MNC的距离……9分 ∵PD⊥平面ABCD，
BC⊥DC ∴BC⊥PC.
即点A到平面MNC的距离为
……12分
20．设数列{an}和{bn}满足a1=b1=6, a2=b2=4, a3=b3=3, 且数列{an+1－an }（n∈N*）是等差数列，数列{bn－2}(n∈N*)是等比数列.
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）是否存在k∈N*，使ak－bk∈（0，）？若存在，求出k；若不存在，说明理由.
解：（I）由已知a2－a1=－2, a3－a2=－1, －1－(－2)=1
∴an+1－an=(a2－a1)+(n－1)·1=n－3
n≥2时，an=( an－an－1)+( an－1－an－2)+…+( a3－a2)+( a2－a1)+ a1
=(n－4)+(n－5) +…+(－1)+(－2)+6 =
n=1也合适. ∴an= (n∈N*) ……………………3分
又b1－2=4、b2－2=2
.而
∴bn－2=（b1－2）·()n－1即bn=2+8·()n…6分
∴数列{an}、{bn}的通项公式为：an= ，bn=2+()n－3
（II）设
当k≥4时
为k的增函数，－8·()k也为k的增函数，而f(4)=
∴当k≥4时ak－bk≥………………10分
又f(1)=f(2)=f(3)=0 ∴不存在k， 使f(k)∈（0，）…………12分
20.已知椭圆，直线l过点A（-a,0）和点B（a,ta）（t>0）交椭圆于M。直线MO交椭圆于N。
（Ⅰ）用a,t表示的面积S；
（Ⅱ）若，a为定值，求S的最大值。
解:（I）易得l的方程为
…1分 由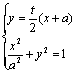
，
得（a2t2+4）y2－4aty=0…2分
解得y=0或
即点M的纵坐标
…………4分
S=S△AMN=2S△AOM=OA·yM=
…7分 （2）由（1）得，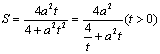
令
…………9分
若1≤a≤2，则
，故当
时，Smax=a…11分
若a＞2，则
在[1，2]上递增，进而S(t)为减函数.
∴当t=1时,
综上可得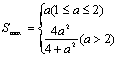
…………14分