高三数学第二学期导师制（04）A

高三数学第二学期导师制（04）

一、填空题：

1．展开式中的系数是　　　　　　 

2． 已知 　　　　 。

3．圆锥曲线 　　　　　　  　。

4．等差数列中，已知，则n为　50 。

5．双曲线虚轴的一个端点为M，两个焦点为F₁、F₂，∠F₁MF₂=120°,则双曲线的的比值为　 。

6．设函数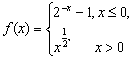若，则x₀的取值范围是 　　　　　　　　 .

7．函数的最大值为 　　　　　 .

8．已知圆的弦长为时，则a=　 　　　　　  .

9． 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，不同的种植方法共　　　　 种　.

10．函数　　　　　　　  .

11．若直线相切，则实数m的值等于　　　　　　.

12．在平面几何里，有勾股定理：“设△ABC的两边AB、AC互相垂直，则AB²+AC²=BC²，

拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面面积间的关系，可

以得出的正确结论是：“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂

直，则　　　　　　　　　　　　　　 。

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上

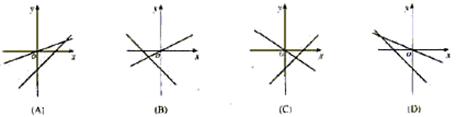
13．在同一直角坐标系中，表示直线y=ax 与y=x+a,正确的是　　　　　　　　 （　　）

14.”是“”的　 　　　　　　　　　 　　　　（　　）

A．必要非充分条件B．充分非必要条件;C．充分必要条件;D．既非充分又非必要条件

15．已知α，β是平面，m，n是直线.下列命题中不正确的是　 　　　　　　　 （　　）

　　A．若m∥n，m⊥α，则n⊥α　B．若m∥α，α∩β=n，则m∥n

　　C．若m⊥α，m⊥β，则α∥β D．若m⊥α，，则α⊥β

16. 某班试用电子投票系统选举班干部候选人.全班k名同学都有选举权和被选举权，

他们的编号分别为1，2，…，k，规定：同意按“1”，不同意（含弃权）按“0”，

令　　

其中i=1，2，…，k，且j=1，2，…，k，则同时同意第1，2号同学当选的人数为（　　）

　　A．； C．；

　　B．； D．

三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。

17．已知函数

　 （Ⅰ）求的最小正周期； （Ⅱ）若，求的最大值、最小值.

解：

 

18．已知数列{a_n}中，a₁=2、(n≥2)，b_n是方程(a_n+1)²x²-2(a_n+1)x+1=0的根；

　 （1）探索数列{a_n}的通项公式并说明理由；

　 （2）设函数（nÎN），求的最小值。

解：

19．如图，正三棱柱ABC—A₁B₁C₁的底面边长的3，侧棱AA₁=D是CB延长线上一点，且BD=BC.

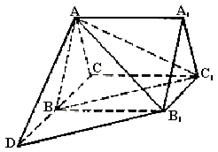
　 （Ⅰ）求证：直线BC₁//平面AB₁D；

　 （Ⅱ）求二面角B₁—AD—B的大小；

　 （Ⅲ）求三棱锥C₁—ABB₁的体积.

20．如图，设定直线L₁：x=-,定点F（，0），其中＞0.动直线L₂垂直L₁与点P，线

　　段PF的垂直平分线交L₂与点M。

　 （1）求点M的轨迹C的方程。

　 （2）设点M的轨迹C与x轴交于点Q，在C上是否一定存在另外两点R、S，使得ΔQRS

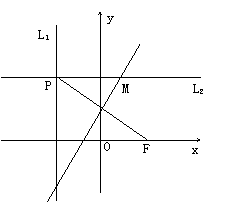　　　 为等边三角形？若存在，请用表示这个等边三角形的面积；若不存在，请说明理由。

解：

高三第二学期导师制（04）解答

一、填空题：

1．展开式中的系数是　　　　　　 

2． 已知 －　 。

3．圆锥曲线 。

4．等差数列中，已知，则n为　50 。

5．双曲线虚轴的一个端点为M，两个焦点为F₁、F₂，∠F₁MF₂=120°,则双曲线的的比值为。

6．设函数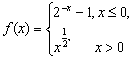若，则x₀的取值范围是（-∞，-1）∪（1，+∞） .

7．函数的最大值为 　.

8．已知圆的弦长为时，则a=　 .

9． 从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，不同的种植方法共　18 种　.

10．函数　　 .

11．若直线相切，则实数m的值等于　　 -3或-13  .

12．在平面几何里，有勾股定理：“设△ABC的两边AB、AC互相垂直，则AB²+AC²=BC²，

拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面面积间的关系，可

以得出的正确结论是：“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂

直，则　　　　　　　　　　　　　　

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上

13．在同一直角坐标系中，表示直线y=ax 与y=x+a,正确的是　　　　　　　　　（ D ）

14.”是“”的　 　　　　　　　　　　　  （  A　）

A．必要非充分条件B．充分非必要条件;C．充分必要条件;D．既非充分又非必要条件

15．已知α，β是平面，m，n是直线.下列命题中不正确的是　 　　　　　 （  B　）

　　A．若m∥n，m⊥α，则n⊥α　B．若m∥α，α∩β=n，则m∥n

　　C．若m⊥α，m⊥β，则α∥β D．若m⊥α，，则α⊥β

16. 某班试用电子投票系统选举班干部候选人.全班k名同学都有选举权和被选举权，他们的编号分别为1，2，…，k，规定：同意按“1”，不同意（含弃权）按“0”，令

　　　　其中i=1，2，…，k，且j=1，2，…，k，则同时同意第1，2号同学当选的人数为（　C　）

　　A．

　　B．

　　C．

　　D．

三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤。

17．已知函数

　 （Ⅰ）求的最小正周期； （Ⅱ）若，求的最大值、最小值.

（Ⅰ）解：因为

所以的最小正周期

（Ⅱ）解：因为所以当时，取得最大值；

当时，取得最小值－1.

所以在上的最大值为1，最小值为－

18．已知数列{a_n}中，a₁=2、(n≥2)，b_n是方程(a_n+1)²x²-2(a_n+1)x+1=0的根；

　 （1）探索数列{a_n}的通项公式并说明理由；

　 （2）设函数（nÎN），求的最小值。

解：

19．如图，正三棱柱ABC—A₁B₁C₁的底面边长的3，侧棱AA₁=D是CB延长线上一点，且BD=BC.

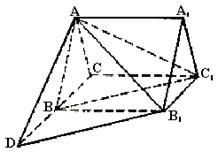
　 （Ⅰ）求证：直线BC₁//平面AB₁D；

　 （Ⅱ）求二面角B₁—AD—B的大小；

　 （Ⅲ）求三棱锥C₁—ABB₁的体积.

 （Ⅰ）证明：CD//C₁B₁，又BD=BC=B₁C₁，

 ∴ 四边形BDB₁C₁是平行四边形， ∴BC₁//DB₁.

又DB₁平面AB₁D，BC₁平面AB₁D，

∴直线BC₁//平面AB₁D.

（Ⅱ）解：过B作BE⊥AD于E，连结EB₁，

∵B₁B⊥平面ABD，∴B₁E⊥AD ，

∴∠B₁EB是二面角B₁—AD—B的平面角，

∵BD=BC=AB，

∴E是AD的中点，

在Rt△B₁BE中，

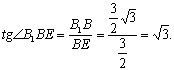∴∠B₁EB=60°。即二面角B₁—AD—B的大小为60°

　 （Ⅲ）解法一：过A作AF⊥BC于F，∵B₁B⊥平面ABC，∴平面ABC⊥平面BB₁C₁C，

∴AF⊥平面BB₁C₁C，且AF=

 即三棱锥C₁—ABB₁的体积为

　　　　解法二：在三棱柱ABC—A₁B₁C₁中，

　即三棱锥C₁—ABB₁的体积为

20．如图，设定直线L₁：x=-,定点F（，0），其中＞0.动直线L₂垂直L₁与点P，线

　　段PF的垂直平分线交L₂与点M。

　 （1）求点M的轨迹C的方程。

　 （2）设点M的轨迹C与x轴交于点Q，在C上是否一定存在另外两点R、S，使得ΔQRS

　　　 为等边三角形？若存在，请用表示这个等边三角形的面积；若不存在，请说明理由。

解：