高三数学百分能力训练八
选择题
1.已知函数f (x)＝sin(x－φ)＋cos(x－φ)为奇函数,则φ的一个取值为 ( )
A.0 B.π C. D.
2.按向量a平移, 将x2＋y2－4x＋2y＋1=0化简为标准方程, 则向量a的坐标是 ( )
A.(－2,1) B.(2,－1) C.(－2,－1) D.(2,1)
3.已知函数y＝f (x) (a≤x≤b), 则集合{(x ，y) y＝f (x), a≤x≤b}∩{( x ，y) x＝0}中含有元素的个数是 A.0 B.1或0 C.1 D.1或2 ( )
4.设F1、F2为椭圆＋y2＝1的两焦点, P在椭圆上, 当△F1PF2面积为1时,PF1·PF2的值为( )
A.0 B.1 C.2 D.
变题: 设F1、F2为双曲线－y2＝1的两焦点, P在双曲线上, 当△F1PF2面积为1时,PF1·PF2的值为( )
A.0 B.3 C.2 D.
5.在地球北纬60º圈上有A、B两点,它们的经度相差180º,则A、B两点沿纬度圈的弧长与A、B两点间的球面距离之比为 ( )
A.3∶2 B.2∶3 C.1∶3 D.3∶1
6. 三人互相传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍回到甲手中,则不同的传球方式共有
A.6种 B.8种 C.10种 D.16种 ( )
7.正四棱锥ABCD－A1B1C1D1的底面边长为1,侧棱长为2,E是AA1的中点,F是BB1中点,则直线EB1与FC1所成的角是 ( )
A.90º B.60º C.45º D.30º
8.已知f (x＋y)＝f (x)＋f (y)且f (1)＝2, 则f (1)＋f (2)＋…＋f (n)不能等于 ( )
A. f (1)＋2 f (1)＋…＋n f (1) B.f [] C.n (n＋1) D. n (n＋1)f (1)
一、填空题
9.已知不等式2x－t＋t－1＜0的解集为(－, ),则t＝ ;
10.已知小张在练习射击时,每次命中目标的概率为 .如果小张连续射击五次,则仅有三次命中且有二次射
击连续命中的概率是 ;
11.设x，y，z中有两条直线和一个平面，已知命题
为真命题，则x，y，z中可能为平面的是
；
12.函数f (x)满足f (x＋3 )＝－,且f (3)＝1,则f (2004)＝ .
二、解答题
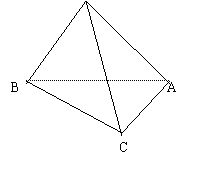
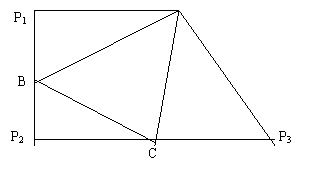
13.如图,三棱锥P－ABC中,AP＝AC,PB＝2,将此三棱锥沿三条侧棱剪开,其展开图是一个直角梯形P1P2P3A．
(1) 求证：侧棱PB⊥AC；
(2)
|
|
 | |||
 | |||
14.P是曲线y＝x n (n为大于1的奇数 )上异于原点的任意一点，过P点的切线分别交x轴、y轴于Q、R两点，交曲线于另一点S．若＝,求的值.
15.(理化类)
给定正整数n,对于满足条件
的等差数列
.记
.求证:
（Ⅰ）
（其中d为公差）;
（Ⅱ）
.
参考答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| D | A | B | A | A | C | B | D |
二、填空题
9. 0 ; 10. 11.x或y 12.－1.
三、解答题
13.解：(1)在平面图中,P1B⊥P1A,P2B⊥P2C,故在三棱锥中,PB⊥PA,PB⊥PC.
∴PB⊥面PAC,∴PB⊥AC.
(2)在三棱锥中作PD⊥AC,垂足为D,连BD,由三垂线定理,得BD⊥AC,
|
|
在展开图中,作AE⊥CP3,垂足为E.
在三棱锥中,设PA＝AC＝x.如图,在平面图中,
CE＝P3E＝.
|
又由P2C＝P3C＝2,且P2E＝P1A,知
|
x＝3.
|
|
|
P3D＝ PD＝.
|
∴cos∠PDB＝.
14. 解：设P (a, a n ),∵f ′(a)＝n an－1,于是切线l：y－a n＝n an－1(x－a)．令y＝0,得xQ＝(1－)a .
又xR＝0,故＝＝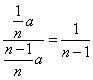
,于是n＝3.
将切线与曲线方程联立,得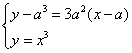
,消去y得xS＝－2a. 故＝
.
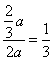15.解: （Ⅰ）证明：
（Ⅱ）由（Ⅰ）得
又
设
，其中
，
则，
.
（式中
）， 