高三数学百分能力训练三
选择题
一、
1. 设![]() 都是非空集合,定义
都是非空集合,定义![]() .若P={1,2,3},Q={4,5},R={6,7,8,9}.则
.若P={1,2,3},Q={4,5},R={6,7,8,9}.则![]() 中元素的个数
( )
中元素的个数
( )
A.6 B.12 C.8 D.24
2.设![]() 均为非零向量,且满足条件
均为非零向量,且满足条件![]() ,
,![]() ,若向量
,若向量![]() .则一定有
( )
.则一定有
( )
A.![]() B.
B.![]() =
=![]()
C.![]() D.
D.![]() =
=![]() 且
且![]()
3.给定性质(1)最小正周期为π;(2)图象关于直线![]() 对称,则下列四个函数中,同时具有性质(1)、(2)的是
( )
对称,则下列四个函数中,同时具有性质(1)、(2)的是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.等比数列![]() 的公比为
的公比为![]() ,则“
,则“![]() ”是“对于任意自然数
”是“对于任意自然数![]()
![]() ,都有
,都有![]() ”的( )
”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
5.对于抛物线![]() 若点
若点![]() 满足条件
满足条件![]() .则称点
.则称点![]() 在抛物线的内部.当点
在抛物线的内部.当点![]() 在抛物线C的内部时,直线
在抛物线C的内部时,直线![]() 与抛物线C的关系是 ( )
与抛物线C的关系是 ( )
A.恰有一个公共点 B.恰有两个公共点
C.有一个或两个公共点 D.没有公共点
6.已知函数![]() 的图像经过点
的图像经过点![]() .
.
记![]() .
.![]()
![]() 则
则![]() 与
与![]() 的大小关系是
( )
的大小关系是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.要完成下列两项调查,⑴从某社区125户高收入家庭,280户中等收入家庭,95户低收入家庭中选出100户调查社会购买力的某项指标.⑵从某中学高三年级的12名体育特长生中选出3人调查学习负担情况,应该采用的抽样方法是 ( )
A.⑴用随机抽样法,⑵用系统抽样法
B.⑴用分层抽样法,⑵用随机抽样法
C.⑴用系统抽样法,⑵用分层抽样法
D.⑴,⑵都用分层抽样法
8.点![]() 上移动,在点
上移动,在点![]() 处切线的倾斜角为
处切线的倾斜角为![]() ,则
,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9. 在![]() 且2m+n=0,mn
且2m+n=0,mn![]() .若它的展开式中系数最大的项是常数项,则
.若它的展开式中系数最大的项是常数项,则![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若![]()
![]() 则
( )
则
( )
A.R<P<Q ; B.P<R<Q ; C.Q<P<R; D.P<Q<R
11.已知△ABC的三个顶点的A、B、C及平面内一
点P满足![]() ,下列结论中正确的
,下列结论中正确的
是 ( )
A.P在△ABC内部 B.P在△ABC外部
C.P在AB边所在直线上D.P是AC边的三等分点
12.三条直线![]() 两两异面,其中,
两两异面,其中,![]() 所成角为
所成角为![]() ,直线
,直线![]() 与
与![]() 所成的角都等于
所成的角都等于![]() .则
.则![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
13.在150°的二面角内,放入一半径为4的球,分
别与两个半平面相切于A、B两点,则A、B间的球
面距离为 .
14.若![]() 的展开式中各项系数的和为128,则展开式中x3项的系数为
.
的展开式中各项系数的和为128,则展开式中x3项的系数为
.
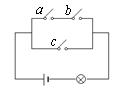 15.如图所示的开关电路中,开关a,b,c开或关的概率都为
15.如图所示的开关电路中,开关a,b,c开或关的概率都为![]() ,且彼此相互独立.则灯亮的概率是
,且彼此相互独立.则灯亮的概率是
.
16.有一密码为631208的手提式保险箱,现在显示的号码为080127,
要打开保险箱,至少需要旋转 步。(每个旋钮上显示的数字可以为0,1,2,3,4,5,6,7,8,9中的任意一个,只要一个旋钮上转出一个新数字就算一步.逆转,顺转都可以).
三、解答题
17.![]()
![]() (2)求
(2)求![]() 的单调增区间;(3)求
的单调增区间;(3)求![]() 的最大值和最小值.
的最大值和最小值.
18. 某班数学兴趣小组有男生和女生各3名,现从中任选2名学生去参加校数学竞赛,求:
(I)恰有一名参赛学生是男生的概率;
(II)至少有一名参赛学生是男生的概率;
(Ⅲ)至多有一名参赛学生是男生的概率.
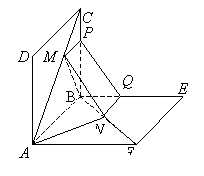
19. 如图,正方形![]() 的边长都是1,而且平面
的边长都是1,而且平面![]() 互相垂直。点
互相垂直。点![]() 在
在![]() 上移动,点
上移动,点![]() 在
在![]() 上移动,若
上移动,若![]() 。
。
(1)求![]() 的长;
的长;
(2)当![]() 为何值时,
为何值时,![]() 的长最小;
的长最小;
|

|
参考答案
一、选择题
1.D提示:确定集合![]() 中的一个元素,由
中的一个元素,由![]() 的取法有3种,
的取法有3种,![]() 的取法有2种,
的取法有2种,![]() 的取法有4种.根据分步计数原理,一共有3×2×4=24个元素.故选D.
的取法有4种.根据分步计数原理,一共有3×2×4=24个元素.故选D.
2.B因为(![]() )
)![]() (
(![]() ).所以,以
).所以,以![]() 为邻边的平行四边形为菱形.因此,
为邻边的平行四边形为菱形.因此,![]() =
=![]() .故选B.
.故选B.
3.D由性质(1)排除A,由性质(2)排除B、C.故选D.
4.A由![]()
1时,同样成立.因此,应选A.
5.D由![]() 方程无实数解,故选D.
方程无实数解,故选D.
6.C由题意得1=![]()
![]()
![]()
所以![]() 故选C.
故选C.
7.B由分层抽样,随机抽样的定义可知,应选B.
8.B![]() .故选B.
.故选B.
9.C![]()
=![]() .
. ,解之得:
,解之得:![]() 故选C. 10.D 11.D
故选C. 10.D 11.D
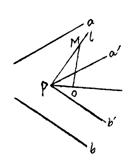 12.B过直线
12.B过直线![]() 上一点
上一点![]() 由
由![]() 所确定的平面的垂线
所确定的平面的垂线![]()
由![]() 又
又
因为异面直线所成的角的最大值为![]() ,应选B.
,应选B.
二、填空题
13.![]() 14.-189
14.-189
15. ![]() 设事件
设事件![]() 关闭时灯亮,即
关闭时灯亮,即![]()
![]()
![]() +
+
![]()
16. 14 由0变6至少需要4步,8变3至少需要5步,由0变1至少需要1步,1变2至少需要1步,由2变0至少需要2步,由7变8至少需要1步.因此,一共至少需要14步.
17.解:(1)![]()
![]()
(2)![]()
![]()
(3)![]()
18.解:基本事件的种数为![]() =15种
=15种
(Ⅰ)恰有一名参赛学生是男生的基本事件有![]() =9种
=9种 ![]() 这一事件的概率P1=
这一事件的概率P1=![]() =0.6
=0.6
(Ⅱ)至少有一名参赛学生是男生这一事件是由两类事件构成的,即恰有一名参赛学生是男生和两名参赛学生都是男生,![]() 所求事件的概率P2=
所求事件的概率P2=![]()
(Ⅲ)至多有一名参赛学生是男生这一事件也是由两类事件构成的,即参赛学生没有男生和恰有一名参赛学生是男生,![]() 所求事件的概率P3=
所求事件的概率P3=![]()
19. (1)作![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,
,![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,依题意可得
,依题意可得
![]() ∥
∥![]() ,且
,且![]()
![]()
![]() ,即
,即![]() 是平行四边形
是平行四边形
∴![]()
![]()
![]()
由已知![]() ,
,![]()
∴![]()
又![]() ,
,![]() ,即
,即![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(Ⅱ)由(Ⅰ),![]()
![]()
![]()
所以,当![]() 时,
时,![]()
![]()
![]()
即![]() 、
、![]() 分别移动到
分别移动到![]() 、
、![]() 的中点时,
的中点时,![]() 的长最小,最小值为
的长最小,最小值为![]() 。
。
(Ⅲ)取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,
,
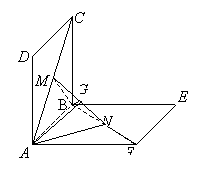
∵![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
∴![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,∠
,∠![]() 即为二面角
即为二面角![]() 的平面角
的平面角
又![]()
![]()
![]()
![]() ,所以,由余弦定理有
,所以,由余弦定理有
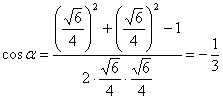
故所求二面角![]() .
.