高三数学试题研究2
1.点A(2,0),B(4,2),若![]() =2
=2![]() ,则点C的坐标为( )
,则点C的坐标为( )
A.(1,-1) B(1,-1)或(3, 1) C(1,-1) 或(3,-1) D无穷多个
2.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
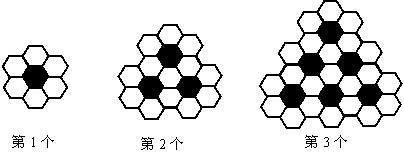 则第n个图案中有白色地面砖
块。
则第n个图案中有白色地面砖
块。
3.已知向量
![]() .
.
(1)求函数![]() 的最小正周期及单调减区间;
的最小正周期及单调减区间;
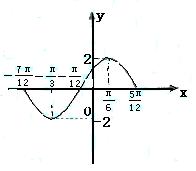
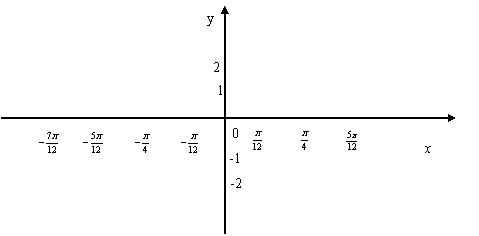
(2)画出函数![]() 的图象,由图象研究并写出
的图象,由图象研究并写出![]() 的对称轴和对称中心;
的对称轴和对称中心;
 (3)是否存在
(3)是否存在![]() ABC,使得A,B是方程
ABC,使得A,B是方程![]() =0的两不等实根?若存在求内角C的大小,若不存在说明理由。
=0的两不等实根?若存在求内角C的大小,若不存在说明理由。
4.已知![]() 是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求 AC 的取值范围.
参考答案:
1.D 2.n2+4n+1
3.解:![]()
![]()
(1)![]()
由 ![]()
![]()
|
|
从图象上可以直观看出,此函数有一个对称中心(![]() ),
),
无对称轴.
(3)不存在,由![]() =0 得:
=0 得:![]() =
=![]() +2k
+2k![]() ,k
,k![]() Z
Z
得方程的解集为![]() ,显然A,B作为三角形内角不属于该集合,所以不存在。
,显然A,B作为三角形内角不属于该集合,所以不存在。
4.(1)解:![]()
依题意![]() 在
在![]() 和[0,2]上有相反的单调性,
和[0,2]上有相反的单调性,
∴x = 0是f (x)的一个极值点,故![]() ,得c = 0
,得c = 0
(2)解:因为f (x)交x轴于点B(2,0)
∴![]() ,即
,即![]()
令![]() 得
得![]()
因为f (x)在[0,2]和[4,5]上有相反的单调性,∴![]() 在[0,2]和[4,5]上有相反的
在[0,2]和[4,5]上有相反的
符号
故2≤![]() ≤4 Þ -6≤
≤4 Þ -6≤![]() ≤-3
≤-3
假设存在点M(x0,y0)使得f (x)在点M的切线斜率为3b,则f / (x0) =3b,
即![]()
![]()
而-6≤![]() ≤-3,∴△<0
≤-3,∴△<0
故不存在点M(x0,y0),使得f (x)在点M的切线斜率为3b.
(3)解:设![]() ,依题意可令
,依题意可令![]()
![]()
则![]() 即
即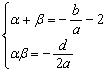
∴![]()
∵-6≤![]() ≤-3,∴当
≤-3,∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,故3≤ AC ≤4
,故3≤ AC ≤4![]()