高三数学题

高三数学题1、在集合中任取一个元素，所取元素恰好满足方程的概率是  。

2、从原点出发的某质点M，按向量移动的概率为，按向量移动的概率为.设M到达点的概率为，求.

解析：M到达点有两种情形：①从点按向量移动到点，此时概率为；②从点按向量移动到点，此时概率为.因这两种情形是互斥的，故有 ，即 .又易得，所以数列是以为首项，为公比的等比数列.

于是.

所以

.

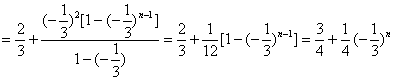3、如图，在南北方向直线延伸的湖岸上有

一港口A.一汽艇以60的速度从

A出发，30分钟后因故障而停在湖里.已

知汽艇出发后先按直线前进，以后又改

成正东方向航行，但不知最初的方向和

何时改变方向.现要去营救，请用图表示营救的区域.

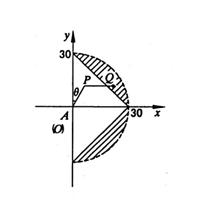
解析：以A为原点，过A的南北方

向所在直线为轴建立坐标系，如图8.

设汽艇的最初航向的方位角为，设沿方向前进千米到达点，然后向东

前进千米到达点发生故障而抛锚.令点的坐标为，则，

且.

.

汽艇中途东拐，.

又

.

点所在区域为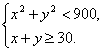

由对称性知如图13的两阴影即为汽艇所在的区域.

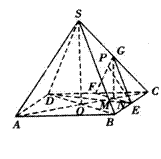
4、在正四棱锥S－ABCD中，E是BC的中点，P点在侧面内及其边界上运动，并且总是保持PEAC.

（1）指出动点P的轨迹（即说明动点P在满足给定的条件下运动时所形成的图形），证明你的结论；

（2）以轨迹上的动点P为顶点的三棱锥P－CDE的最大体积是正四棱锥S－ABCD体积的几分之几？

（3）设动点P在G点的位置时三棱锥P－CDE的体积取最大值V₁，二面角G－DE－C的大小为，二面角G－CE－D的大小为，求的值.

（4）若将“E是BC的中点”改为“E是BC上异于B、C的一定点”，其它条件不变，请指出点P的轨迹，证明你的结论.

解析：（1）如图，分别取CD、SC的中点F、G，连结EF、EG、FG、BD.设AC与BD的交点为O，连结SO，则动点P的轨迹是的中位线FG.

由正四棱锥可得.又

平面EFG，平面EFG，.

（2）由于是定值，所以当P到平面CDE的距离最大时，最大，易知当P与G重合时，P到平面CDE的距离最大，故.又，G到平面ABCD的距离是点S到平面ABCD的距离的，

.

（3）令，EF与AC交于N点，连结GN，则GN平面ABCD.

因此二面角G－DE－C和二面角G－CE－D的平面角的正切值的比就等于N到DE和CE的距离的倒数比.

N是OC的中点，N到BC的距离为.

连结DE交OC于M，则M是的重心，.

又，

在中，容易求得N到DE的距离为.

故.

（4）动点P在侧面SCD内部及其边界上运动，且总保持，那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内，而由正四棱锥的性质可知，平面SBD，因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作E//SB，E//BD，分别交SC于，交CD于，则平面E//平面SBD，从而平面E，故点P的轨迹是线段.

说明：本题全方位地考查了立体几何中的主要内容，如线面与线线的位置关系、体积问题、二面角问题等.在立体几何的问题中给出了探求点的轨迹问题，与平面几何、解析几何紧密联系，体现了对综合运用知识的能力要求，考查的知识点丰富，具有相当的难度和深度，达到了压轴题的水平，是一道优秀的创新型试题.