高三数学题目3

1．  高三数学题目3（石中）已知数列｛a｝、｛b｝满足a=2t(t为常数且t≠0) ,且a=2t-, b=　　（1）判断数列｛b｝是否为等差数列，并证明你的结论。

　 （2）若b= b+,作数列｛d｝,使d=2,d=f(d)(nN),

求和A=Cd+Cd+…+Cd。

解：（1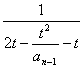）b=====-=+b,

∴b- b=,　 ∴｛b｝是等比数列。

（2）b-b==，∴f(t)=2t, ∴d=f(d)=2d,又d=2

∴｛d｝是首项为2，公比为2的等比数列，即d=2

即A=2C+2C+…+2C=C+2C+2C+…+2C-1=3-1.

2. （石中）设平面向量=(2,-1),=(2,4)，若存在实数m和，使向量=+(2sin-3),=-m+sin且⊥.

（1）求函数m=f()的关系式.

（2）求m的最大值和最小值

解：（1）∵=(2,-1),=(2,4),

﹒=2×2+(-1)×4=0, ｜｜=2+(-1)=5, ｜｜=2+4=20

﹒=〔+(2sin-3)〕﹒(-m+sin)

=-ma+(2sin-3sin)=-5m+20(2sin-3sin)

又∵⊥,∴﹒=0,即-5m+20(2sin-3sin)=0

∵m=4(2sin-3sin),即f()=4(2sin-3sin).

（2）设sin=t，则m=4(2t-3t),(t﹝-1,1﹞),

令g(t)= 2t-3t (t﹝-1,1﹞), 则(t)=6t-3,

令(t)=0，可得t=,当t变化时，g(t) ，(t)的变化情况如下表：

t	﹝-1,-﹚	-	(-,)		(,1﹞
(t)	+	0	-	0	+
g(t)	↗	极大值	↘	极小值-	↗

又g(1)=-1,g(-1)=1,故g(t)的最大值为，最小值为-，

∵m的最大值为4，最小值为-4。

3．（石中）平面直角坐标系中，O为坐标原点，已知A（3，1），B（-1,3），若点C满足，其中，且，则点C的轨迹方程为_______. 答案：（x+2y-5=0）

4．（石中）已知曲线C：. 给出下列命题：

　　　 　①0<k<1时，曲线C是焦点在x轴上的双曲线；

②k =1 时，曲线C是抛物线；

③1<k<2时，曲线C是焦点在y轴上的椭圆；

④k >2时，曲线C是焦点在x轴上的椭圆。其中正确命题的序号是_______（注：把你认为正确的命题的序号都填上）。答案：(2)(3)