高三数学题选编2

高三数学题选编2

1．一水池有2个进水口，1 个出水口，进出水速度如图甲、乙所示. 某天0点到6点，该水池的蓄水量如图丙所示.（至少打开一个水口）

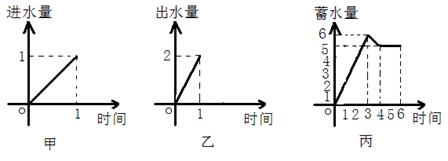
给出以下3个论断：

①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水.则一定能确定正确的论断是　

A．①　　　　　 B．①②　　　　　　　　 C．①③　　　　　　　 D．①②③

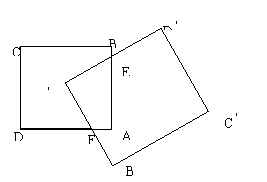2．如图所示，正方形ABCD的中心是A，ABCD也是正方形，若正方形ABCD的面积是1，且AB>AB，AE>BE，两正方形的公共部分四边形AEAF的面积为S，则

　　　 A．S=　　　　　　　 B．S>

　　　 C．S<　　　　　　　 D．S的大小由正方形ABCD的大小与AE的大小而定

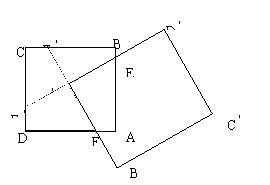A　　　　　　如图，延长DA交CD于E，延长BA交BC于F，则根据对称性，正方形被分成四个全等的四边形。

3． 把正奇数数列中的数按上小下大、左小右大的原则排成如下三角形数表：

1

3　　5

7　　9　 11

—　　—　　—　　—

　　—　　—　　—　　—　　—

　　设是位于这个三角形数表中从上往下数第行、从左往右数第个数。

　　（I）若，求的值；

　　（II）已知函数的反函数为　，若记三角形数表中从上往下数第n行各数的和为，求数列的前n项和。

解：（I）三角形数表中前行共有个数，

　　第行最后一个数应当是所给奇数列中的第项。

故第行最后一个数是　　　　　

因此，使得的m是不等式的最小正整数解。

　　由得

　　

　　于是，第45行第一个数是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　（II），。

　　故　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　第n行最后一个数是，且有n个数，若将看成第n行第一个数，则第n行各数成公差为-2的等差数列，故。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　故

　　，

　　两式相减得：

　　　　　　　　　　　　　

　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　

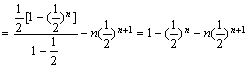
4． A有一只放有x个红球，y个白球，z个黄球的箱子（x、y、z≥0，

且），B有一只放有3个红球，2个白球，1个黄球的箱子，两人各自从自

己的箱子中任取一球比颜色，规定同色时为A胜，异色时为B胜.

　 （1）用x、y、z表示B胜的概率；

　 （2）当A如何调整箱子中球时，才能使自己获胜的概率最大？

解：（1）显然A胜与B胜为对立事件，A胜分为三个基本事件：

①A₁：“A、B均取红球”；②A₂：“A、B均取白球”；③A₃：“A、B均取黄球”.

（2）由（1）知，

于是，即A在箱中只放6个红球时，获胜概率最大，其值为