高三数学统练十三
一、选择题（每题5分 共40分）
1．在数列
中，
则该数列中相邻两项乘积是负数的项是（ ）
（A）
和
（B）和
（C）和
（D）和
2．数列中，
，又数列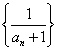
是等差数列，则
=（ ）
（A）0
（B）
（C）
（D）－1
3．等比数列{an}中，设a9=－2, 则此数列的前17项之积为（ ）。
（A）216 （B）－216 （C）217 （D）－217
4．一张报纸，其厚度为a，面积为b，现将此报纸对折（既沿对边中点的连线折叠）7次，
这时报纸的厚度和面积分别是 （ ）
A．
B．
C．
D．
5．已知
顺次成等差数列，则（
）
（A）
有最大值，无最小值
（B）有最小值
，无最大值
（C）有最小值，最大值1 （D）有最小值 -1，最大值1
6．设数列
是公比为a（a≠1）首项为b的等比数列，Sn是前n项和，对任意的n∈N，点（
） （ ）
A．在直线
上 B．在直线
上
C．在直线
上 D．在直线
上
7．设双曲线
中，离心率
，则两条渐近线的夹角
θ的取值范围是 （ ）
A．
B．
C．
D．
8、当
则函数
的最大值是（ ）
（A）9 （B）81 （C）64 （D）6
二、填空题 （每题5分 共30分）
9．在等差数列中，若
则
等于
.
10．Sn表示数列{an}前n项的和，若对任意n∈N，恒有9Sn=10an+9(n+10)，则通项公式an=
11．已知正方体的八个顶点中，有四个点恰好为正四面体的顶点，则该正四面体的体积与正方体的体积之比为
12．已知函数
，满足
则
13．设
，下列命题
①既不是奇函数，又不是偶函数
②若x是三角形内角，则是增函数
③若x是三角形内角，则有最大值无最小值
④的最小正周期为π
其中正确命题序号是
14．已知数列{an}是公比大于1的等比数列，Sn是它的前n项的和，Tn是它的前n项的倒数和，且
=
, 则满足Sn>Tn的最小自然数n
高三数学统练十三
2004.2.24
班级___________ 姓名_____________ 学号____________ 成绩___________
一、选择题（每小题5分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
|
|
|
|
|
二、填空题（每小题5分，共30分）
9． 10.
11． 12.
13． 14.
三、解答题
15、（本题满分8分）三个互不相同的实数是等比数列{an}中的连续三项，又依次为某一等差数列中的第2项，第9项和第44项，这三个数的和为217。
（1）求这三个数；
（2）记Sn为等比数列{an}的前n项和，且
＜
＜
，求n的值。
16．（本题满分10分）
已知△ABC中，A、B、C分别是三个内角，a、b、c分别是角A、B、C的对边，已知
的外接圆的半径为
.
（Ⅰ）求角C （Ⅱ）求△ABC面积S的最大值.
17．（本题满分12分）
已知二次函数
的图象的顶点坐标是
（Ⅰ）求
的表达式，并求出f（1）、f（2）的值；
（Ⅱ）数列{an}，{bn}，若对任意的实数x都满足
，
其中
是定义在实数R上的一个函数，求数列{an}，{bn}的通项公式；
（Ⅲ）设圆
，若圆Cn与圆Cn+1外切，{rn}是各项都是正
数的等比数列，记Sn是前n个圆的面积之和，求
.
18．（附加题）（本小题满分14分）已知函数
对任意实数x、y都有
（1）若t为自然数，试求f(t)的表达式；
（2）满足条件f(t)= t的所有整数t能否成等差数列？若能构成等差数列，求出此数列；若不能构成等差数列，请说明理由；
（3）若对于t≥4的所有自然数，
恒成立，求m的最大值
答案：CBDC BDBB 9、100 10、an=－100×10n－1+1 11、1:3
12、4006 13、①③ 14、10
15．（1）设这三个数为
，则
即
又
，即
由①②得
所求三数为7，35，175
----------------4分
（2）由（1）知等比数列的公比为5，故
，于是由＜＜，得＜
＜
＜
＜
，由于n为整数，
n = 3.
----------------8分
16．解：（I）
，由正弦定理得：
……………2分
由余弦定理得：
………5分
（II）
……………………………………………………7分
，
………………………………………………………………10分
法2：
……4分
=
…………………………………8分
当
………………………………………10分
17．解：（I）由已知得
…………………………4分
（II）
①
②
由①②得
…………………………………………8分
（III）
，设数列{rn}的公比为q，则
………10分
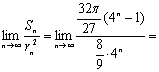
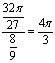……………………………………………12分
18、解：（1）
……1分
当t为自然数时，让t从1，2，3，……t－1取值有
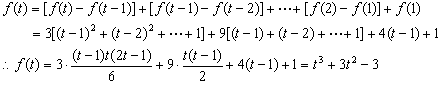
当t为自然数时，f(t)的解析式为
……5分
（2）当
当t=0时，在
中，令
知 
综上所述，当
……8分 
成等差数列，此数列为1，－1，－3或－3，－1，1
……………… 10分
（3）当
时，
，由
恒成立知
恒成立
∴m的最大值是3
……14分