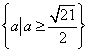高三数学交流题

高三数学交流题

1．某城市各类土地单位面积租金y（万元）与该

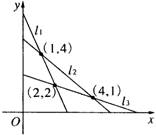地段离开市中心的距离x（km）关系如图所示，

其中l₁表示商业用地，l₂表示工业用地，l₃表

示居住用地，该市规划局单位面积租金最高为

标准规划用地，应将工业用地划在（　　）

　　　 A．与市中心距离分别为3km和5km的圆环区域内

　　　 B．与市中心距离分别为1km和4km的圆环形区域内

　　　 C．与市中心距离为5km的区域外

　　　 D．与市中心距离为5km的区域内

答：B

2．设坐标平面内有一个质点从原点出发，沿x轴跳动，每次向正方向或负方向跳1个单

位，经过5次跳动质点落在点（3，0）（允许重复过此点）处，则质点不同的运动方法共有

　　　　 种（用数字作答）。　　　　　　　　　　　　　　　　　　　　　 答：5

3．某渔业公司年初用98万元购买一艘捕鱼船，第一年各种费用为12万元，以后每年都增加4万元，每年捕鱼收益50万元．

（1）问第几年开始获利?

　　（2）若干年后，有两种处理方案：

　　方案一：年平均获利最大时，以26万元出售该渔船

　　方案二：总纯收入获利最大时，以8万元出售该渔船．问哪种方案合算．

解析：（1）由题意知，每年的费用以12为首项，4为公差的等差数列．

　　设纯收入与年数n的关系为f（n），则

　　…．

　　由题知获利即为f（n）＞0，由，得．

　　∴　2.1＜n＜17.1.而nN，故n＝3，4，5，…，17．

　　∴　当n＝3时，即第3年开始获利．

　　（2）方案一：年平均收入．

　　由于，当且仅当n＝7时取“＝”号．

　　∴　（万元）．

　　即第7年平均收益最大，总收益为12×7＋26＝110（万元）．

　　方案二：f（n）＝＋40n-98＝-2＋102．

当n＝10时，f（n）取最大值102，总收益为102＋8＝110（万元）．

　　比较如上两种方案，总收益均为110万元，而方案一中n＝7，故选方案一．

4．已知集合,

，是否存在正实数，使得，如果存在求的集合？如果不存在请说明理由。

解：∵　　∴

将代入得

设

令

当时　

依题意得　　∴

∴适合条件的存在其集合为