高三数学联考测试卷

高三数学联考测试卷

　　　　　　

本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟

第I卷（选择题，共60分）

参考公式：

如果事件A、B互斥，那么

P（A+B）=P（A）+P（B）

如果事件A、B相互独立，那么

P（A·B）=P（A）·P（B）

如果事件A在一次试验中发生的概率是p，那么n次独立重复试验中恰好发生k次的概率

　　

正棱锥、圆锥的侧面积公式

其中c表示底面周长，l表示斜高或母线长，球的体积公式

其中R表示球的半径

一、选择题（本大题共12个小题，每小题5分，共60分，在每小题的四个选项中，只有一项是符合题目要求的）

1. 如果集合，，则（　　）

A. 　　　　 B. 　　　　C. S = T　　　　D. S≠T

2. 已知三个实数a，b = a^a，c = a^b，其中0.9﹤a﹤1，则（　　）

A. a﹤c﹤b　　　 B. a﹤b﹤c　　　 C. b﹤a﹤c　　 D. c﹤a﹤b

3. 当x–2﹤a时，不等式x²– 4﹤1成立，则正数a的取值范围是（　　）

）

]

A.（）　B.（　 C. [　D. （）

4. 在平面内有△ABC和点O，且，则点O是△ABC的（　 ）

A. 重心　　　　  B. 垂心　　　　 C. 内心　　　　　 D. 外心

5. 两直线与椭圆（q是参数）的四个交点为顶点的四边形的面积是（　　）

A. 　　　　　B. 　　　　C. 　　　　D. 24

6. 设等比数列{a_n}满足条件：对任何正整数n，其前n项和S_n恒等于a_n+1 – a₁，则这样的等比数列（　　）

A. 不存在

B. 必定存在，其公比可定，但首项不定

C. 必定存在，其首项可定，但公比不定

D. 必定存在，但首项与公比均不定

7. 若a﹥3，则方程x³ – ax² + 1 = 0在（0，2）上恰有（　　）

A. 0个根　　　　 B. 一个根　　　　C. 2个根　　　D. 3个根

8. 正方体ABCD–A₁B₁C₁D₁中，E、F分别是AA₁与CC₁的中点，则直线ED与直线D₁F所成角为（　　）

A. 　　　 B. 　　　　　C. 　　　　　D.

≥

9. 对于函数，下列命题中正确的是（　　）

A. 该函数的值域为[–1，1]

B. 当且仅当时，函数取最大值1

C. 函数是以p为最小正周期的函数

D. 当且仅当时，f（x）﹤0

10. 在平面内将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点（–2，4）重合. 若点（5，8）与点（m，n）重合，则m+n的值为（　　）

A. 4　　　　  B. – 4　　　　　　  C. 13　　　　　　　 D. –13

11. 身高互不相同的6个人排成2横行3纵列，在第一行的每个人都比他同列的身后的人个子矮，则所有不同排法的种数为（　　）

A. 15　　　　 B. 84　　　　　　  C. 90　　　　　　　 D. 540

12. 已知4枝郁金香和5枝丁香的价格之和小于22元，而6枝郁金香和3枝丁香的价格之和大于24元. 设2枝郁金香的价格为a元，3枝丁香的价格为b元，则a，b大小为（　　）

A. a﹥b　　　 B. a = b　　　　　  C. a < b　　　　　　  D.不确定

第Ⅱ卷（非选择题，共90分）

二、填定题（本大题共4小题，第小题4分，共16分，把答案填在题中横线上）

13. 地球半径为R，在北纬60°圈上有甲、乙两地，它们在纬度圈上弧长为，则甲、乙两地球面距离为　　　　　　  .

14. 已知x + y = 1（x﹥0，y﹥0），求的最小值，请仔细阅读下列解法，并在填空处回答指定问题.

　  解：∵x + y = 1(x > 0，y > 0)　∴令x = cos²q，y = sin²q（其中①　　　　②　　　　）

≥

则

此时当③　　　　 时，取得最小值.

说明：①指出运用了什么数学方法　②指出q 的一个取值范围　③指出x、y的取值

15. 有下列命题：①x，yÎR，若x²+y²=0，则x、y全为零；②“全等的三角形是相似三角形”的否命题；③“若m﹥1，则mx²–2（m+1）x+m–3﹥0的解集为R”的逆命题；④“若a+5是无理数，则a是无理数”的逆否命题. 其中正确的是　　　　　  .（填上所有正确命题的序号）

16. 已知两台独立运行的仪器发生故降的概率为P₁，P₂，现同时对这两台仪器做运行情况检测，检测中发生故障的仪器台数x的期望是　　　　　 .

三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）

17. （本小题满分14分）

已知，（1）化简f（x）；（2）若，且，求f（x）的值.

18. （本小题满分12分）

从汽车站驾车至汽车西站的途中要经过8个交通岗，假设某辆汽车在各交通岗遇到红灯的事件是独立的，并且概率都是. 求：

（1）这辆汽车首次遇到红灯前，已经过了两个交通岗的概率；

（2）（理科）这辆汽车在途中遇到红灯数x的期望与方差；

（文科）这辆汽车在途中恰好遇到4次红灯的概率.

19. （本小题满分12分）

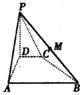如图，四棱锥P–ABCD中，PD⊥面ABCD，PA与平面ABCD所成的角为60°，在四边形ABCD中，∠D=∠DAB=90°，AB=4，CD=1，AD=2，（1）求异面直线PA与BC所成的角；（2）若PB的中点为M，求证：平面AMC⊥平面PBC.

20. （本小题满分12分）

≥

若存在正实数x，使得不等式成立，求实数k的取值范围.

21. （本小题满分12分）

设椭圆C₁方程为（a﹥b﹥0），曲线C₂方程为，且曲线C₁与C₂在第一象限内只有一个公共点P.

（1）试用a表示点P的坐标；

（2）设A、B是椭圆C₁的两个焦点，当a变化时，求△ABP面积函数S（a）的值域；

（3）记min{y₁，y₂，…，y_n}为y₁，y₂，…，y_n中最小的一个，设g（a）是以椭圆C₁的半焦距为边长的正方形的面积，试求函数f（a）=min{ g（a），S（a）}的表达式.

22. （本小题满分14分）

在正三棱锥中，如果以侧棱与底面所成角的余弦值为自变量x，以侧面与底面所成角的余弦值为因变量y，则得到函数y=f（x）.

（1）求函数y=f（x）的解析式及定义域；

（2）判断f（x）的单调性并给予证明；

（3）如果数列{a_n}，，a_n+1= f（a_n）（nÎN^*），求证：当n≥2时，.

参考答案

一、选择题

1. 对S中的n分类：n = 2k，kÎZ则x = 4k+1；n = 2k–1，kÎZ时，x = 4k–1，所以S = T，故选C.

2. 利用指数函数y = a^x（0﹤a﹤1）的单调性比较可知选A.

≤

3. 不等式x–2﹤a的解集为（2–a，2+a），不等式x²–4﹤1的解集为. 由题设知前一解集为后一解集的子集，所以有2–a≥且2 + a ≤所以，故选B.

4. 由知即，所以，同理可得，，所以O是△ABC的垂心，故选B.

5. 椭圆为. 与椭圆在第一象限的交点坐标为，故所求四边形面积为，故选C.

6. 由题设知a₁+a₂+…+a_n=a_n+1–a₁，当公比q=1时，na₁=0，∴a₁=0不符合，所以q≠1，此时有∴1–q=–1，∴q=2，故选B.

7. 令f（x）=x³ – ax² + 1. 则（x）=3x²–2a，在a﹥3，xÎ（0，2）时，（x）﹤0，又f（0）=1﹥0，f（2）= 9 – 4a﹤0，故f（x）的图象在（0，2）上与x轴有一个交点，即f（x）=0有一个根，故选B.

8. 连B₁F，则B₁F∥DE，所以∠D₁FB为异面直线ED与D₁F所成的角. 令正方体棱长为2，则，，，∴,∴，故选A.

9. 由图形可知选D.

10. 由题可知（2，0）与（–2，4）是某一直线的对称点，此直线即为其垂直平分线l：y–2=x，且点（5，8）与（m，n）关于l对称，故可求得m=6，n=7，∴m+n=13，故选C.

11. 由题设知为，故选C.

12. 由二元一次不等式表示的区域可知选A.

二、填空题

13. 甲、乙直线距离为R，在大圆中甲、乙劣弧所对圆心角为，所以甲、乙球面距离为.

14. ①换元法　　②q Î（0，）　　③，

15. ①④

16. P₁+P₂

三、解答题：

17. （1）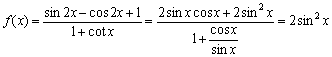

（2）∵，∴　∴，

∴

∴

18. （1）∵这辆汽车在第一、二交通岗均未遇到红灯，而在第三个交通岗遇到红灯，∴

（2）（理）∵x~B（8，）　　∴，

（文）

19. （1）建立如图所示的空间直角坐标系

∵∠D =∠DAB = 90°，AB = 4，CD = 1，AD = 2

∴A（2，0，0），C（0，1，0），B（2，4，0）

由PD⊥面ABCD，得∠PAD为PA与平面ABCD所成的角

∴∠PAD = 60°

在Rt△PAD中，由AD = 2得PD =，∴P（0，0，）

∵=（2，0，），=（–2，–3，0）

∴cos﹤，﹥=

∴与BC所成的角为

（2）∵M为PB中点：M坐标为（1，2，）

∴=（–1，），=（1，1，），=（2，4，）

∵·=（–1）×2+2×4+×=0

·=1×2+1×4+×（）=0

∴⊥，⊥

∴PB⊥面AMC

∵PCÌ面PBC

∴面AMC⊥面PBC

≥

20. ∵

≤

∴

≥

存在正实数x，使得不等式成立

≤

等价于不等式在（0，+¥）内有解

设

则

∴当0﹤x﹤1时，（x）﹥0，f（x）是增函数

当x﹥1时，（x）﹤0，f（x）是减函数

∴当x﹥0时，f（x）有最大值f（1）=ln 2

≤

∴在使在（0，+¥）内有解

即ln k≤ln 2　　　∴0﹤k≤2.

21. （1）由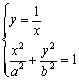得b²x⁴–a²b²x²+a²=0，由条件有△=a⁴b⁴– 4a²b²=0得ab=2，解得或（舍）

∴P点坐标为

（2）∵在△ABP中，，高为

∴

∵a﹥b﹥0，　∴，即

得于是0﹤S（a）﹤

故△ABP面积函数S（a）的值域为（0，）

（3）g（a）= c² = a² – b² = a² –

解不等式g（a）≥S（a）即a²–≥　　

整理得a⁸–10a⁴+24≥0

∴a≥或a≤（舍）

≤

故f（a）=min{ g（a），S（a）}=

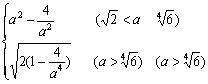
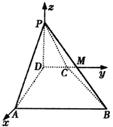
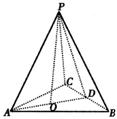22. （1）如图，正三棱锥P–ABC，侧棱长为b，底边长为a，过P作PO⊥面ABC，垂足为O. 连结AO并延长交BC于D. 连结PD，则AD⊥BC，PD⊥BC

在△ABC中，，∴. 在Rt△POA中，

在Rt△PCD中，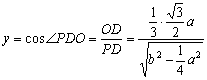

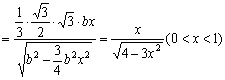
（2）f（x）在（0，1）上是增函数，证明略

（3）

∴，即

∴是首项为8，公比为4的等比数列

∴=8×4^n–1 = 2²ⁿ⁺¹

∴，很明显{a_n}是单调递减数列

∴a_n≤