高三数学模拟试卷4
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.
 |
第Ⅰ卷（选择题 共60分）
注意事项：
1、 答第Ⅰ卷前，考生务必将自己的姓名、班级、考号填写在规定的地方。
2、 每小题选出答案后，用铅笔把答题卡上对应题目的答案方框涂黑，如需改动，用橡皮擦干净后，再选出其他答案，不能答在试卷上。
3、 考试结束后，将答题卡及试卷第Ⅱ卷一并收回。
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 集合A={0，1，2}满足条件
的集合B共有（ ）
A．3个 B．6个 C．7个 D．8个
2.要使函数ｙ＝ｘ２－２ａｘ＋１在［１，２］上存在反函数，则a的取值范围是（ ）
A．ａ≤１ B．ａ≥２ C．ａ≤１或ａ≥２ D．１≤ａ≤２
3.有一件商品的成本为1000元，若在月初出售，可获利100元，然后将本利存入银行(已知银行月息为2%)；若在下月初出售，可获利120元，但要付5元保管费，则（ ）
A.本月初出售获利大
B.在下月初出售获利大
C.在本月初出售和在下月初出售获利相同
D.在本月初出售和在下月初出售获利大小不能确定
4.已知椭圆的焦点是F1、F2，P是椭圆上的一个动点，如果延长F1P到Q，使得
，那么动点Q的轨迹是 （ ）
A 圆 B 椭圆 C 双曲线的一支 D 抛物线
5. 对于二项式
，四位同学作出了四种判断：
①存在
，展开式中有常数项；
②对任意，展开式中没有常数项；
③对任意，展开式中没有x的一次项；
④存在，展开式中有x的一次项。
上述判断中正确的是 （ ）
A.①与③ B ②与③ C ②与④ D ④与①
6.二00五年度参加大学学科能力测验的有12万名学生，各学科成绩采用15级分，数学学科能力测验成绩分布图如下图：请问有多少考生的数学成绩分高于11级分？选出最接近的数目（ ）
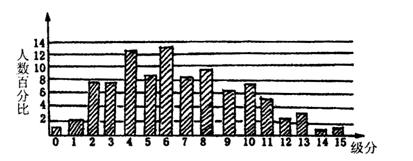
A．4000人 B．10000人 C．15000人 D．20000人
7.椭圆
和圆
交于四个不同点，则椭圆离心率的取值范围是
（ ）
A．
B． C． 
D．
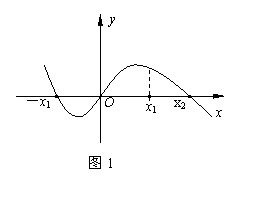
8.设函数f(x)=ax3+bx2+cx+d的图象如右图所示，则
f(－1)+f(1) （ ）
A．大于0 B． 小于0 C．等于0 D．以上结论都有可能
9.给出四个命题，则其中正确命题的序号为 （ ）
①存在一个△ABC，使得sinA+cosA=－1;
②△ABC中,A＞B的充要条件为sinA＞sinB;
③直线x=
是函数y=sin(2x+
)图象的一条对称轴；
④△ABC中，若sin2A=sin2B,则△ABC一定是等腰三角形.
A.①② B.②③ C.③④ D.①④
10. 已知抛物线ｙ＝ｘ２－１上一定点Ａ（－１，０）和两动点P、Q，当ＰＡ⊥ＰＱ时，点Q的横坐标的取值范围是 （ ）
Ａ.（－∞，－３）Ｂ.［１，＋∞］Ｃ.（－３，１）Ｄ.（－∞，－３]∪［１，＋∞)
11.从10种不同的作物种子中选出6种放入6个不同的瓶子中展出，如果甲、乙两种种子不能放入第1号瓶内，那么不同的放法共有（ ）
A．
种 B．
种 C．
种 D．
种
12.给出下面四个命题：①“直线a、b为异面直线”的充分非必要条件是：直线a、b不相交；②“直线l垂直于平面
内所有直线”的充要条件是：l⊥平面；③“直线a⊥b”的充分非必要条件是“a垂直于b在平面内的射影”；④“直线∥平面
”的必要非充分条件是“直线a至少平行于平面内的一条直线”．其中正确命题的个数是（ ）
A．1个 B．2个 C．3个 D．4个
海门市高三数学模拟试卷4
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 1~12 | 13~16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 得 分 | |||||||||
第Ⅱ卷（非选择题，共90分）
|
|
13．已知f(x)=｜ｌｏｇ３ｘ｜当０＜ａ＜２时，有ｆ（ａ）＞ｆ（２），则a的取值范围是 .
14．
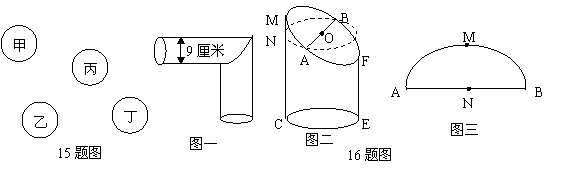如图，甲、乙、丙、丁为湖中四个亭子，要建3座小桥将四个亭子连接起来，不同的建桥方案共有_________种.
15.如图一，现要用铁片做成一个直角烟筒弯头（两个圆柱呈垂直状），烟筒的直径为9cm，沿最短母线EF将侧面展开后，铁片在接口处展开图的轮廓线AMB是正弦曲线的一部分（如图二）.以半圆ANB展开所得的直线为x轴，最长母线CM所在直线为y轴，建立直角坐标系，则此正弦曲线的函数表达式为 .
16．若数列
，
是等差数列，则有数列
也为等差数列，类比上述性质，相应地：若数列
是等比数列，且
，则有
__________也是等比数列．
|
17．（本小题满分12分）
已知函数
的大小. 
|
18．（本小题满分12分）
一次数学考试中有6道选择题，每道选择题有4个选择项，有且仅有1个选择项正确。每题都任选1个选择项填入。
(1) 求恰好答对4道题的概率；
(2) 求恰好答错1题，但不是第1道题的概率；
(3) 求答对多少题的概率最大？
|
19．（本小题满分12分）
已知：
（a＞1＞b＞0）．
（1）求
的定义域；
（2）判断在其定义域内的单调性；
（3）若在（1，＋∞）内恒为正，试比较a-b与1的大小．
|
20．（本小题满分12分）
假设A型进口车关税税率在2002年是100％，在2007年是25％，2002年A型进口车每辆价格为64万元（其中含32万元关税税款）．
（1）已知与A型车性能相近的B型国产车，2002年每辆价格为46万元，若A型车的价格只受关税降低的影响，为了保证2007年B型车的价格不高于A型车价格的90％，B型车价格要逐年降低，问平均每年至少下降多少万元？
（2）某人在2002年将33万元存入银行，假设银行扣利息税后的年利率为1.8％（5年内不变），且每年按复利计算（上一年的利息计入第二年的本金），那么5年到期时这笔钱连本带息是否一定够买按（1）中所述降价后的B型车一辆？
|
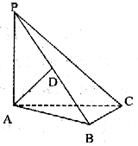
21．（本小题满分12分）
如图三棱锥P-ABC中，PA⊥底面ABC，PA=AB,∠ABC=90°，2BC=AC，D为PB中点。
（1） 求异面直线AD与PC所成角的大小；
（2） 求二面角A-PC-B的正弦值。
|
22．（本小题满分14分）
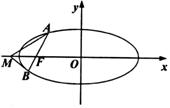如图，过椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”。
（1）求椭圆的“左特征点”M的坐标；
（2）试根据（1）中的结论猜测：椭圆的“左特征点”M是一个怎样的点？并证明你的结论。