高三数学模拟试卷（一）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。
考试时间120分钟。
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（
）=P（
B）
如果事件A在一次试验中发生的概率是P.那么n次独立重复试验中恰好发生k次的概率
（k=0,1,2,3,…n）
第Ⅰ卷
一、 单项选择题（本大题共12小题，每小题5分，共60分）
1．从集合M={不大于10的正自然数}中，选取三个数，使这三个数组成公差d=-3的等差数列，则这样的等差数列一共有
（A）2个 （B）3个 （C）4个 （D）5个
2．设A=
，B=
，则A∩B等于
（A）0 （B）{0} （C）Φ
（D）
3．四面体的四个表面中，直角三角形的个数最多有
（A）1个 （B）2个 （C）3个 （D）4个
4．
是函数
为偶函数的
（A） 充分不必要条件 （B）必要不充分条件
（C） 充分必要条件 （D）既不充分也不必要条件
5．若函数
对任意实数x都有
，那么
的值等于
（A）-2 （B）2 （C）±2 （D）不能确定
6．已知函数f（x）满足f（x+1）=
+f（x）（x∈R），且f（0）=1。则数列{f（n）}前20项的和为
（A）305 （B）315 （C）325 （D）335
7．轴截面为正方形的圆柱，其侧面积为8π，则这个圆柱的内切球表面积等于
（A）8π （B）
（C）
（D）
8．函数
的一个单调递增区间是
（A）
（B）
（C）
（D）
9．设ap、aq是数列{an}的任意两项（p，q，n∈N+），且ap=aq+2003（p-q），那么数列{an}
（A）不是等差数列 （B）是等差数列 （C）可能是等比数列 （D）是常数列
10．两个正数a、b的等差中项是5，等比中项是4。若a＞b，则双曲线
的离心率e等于
（A）
（B）
（C）
（D）
11．有一组数据
。如果将它们改变为
，其中C≠0。则下列结论正确的是
（A）平均数与方差都不变 （B）平均数与方差都改变
（C）平均数改变，方差不变 （D）平均数不变，方差改变
12．已知函数
。当
时，使
恒成立的函数是
（A）
（B）
（C）
（D）
第Ⅱ卷（非选择题共90分）
二、 填空题（本大题共4小题，每小题4分，共16分，把答案填在答卷对应题后的横线上）
13．若不等式
的解集是
，则
=
。
14．已知直角坐标平面内两点
，那么这两点之间距离的最小值等于
。
15．设
，则
。
16．设F1，F2是椭圆
两个焦点，P是椭圆上一点，且PF1-PF2=1，若∠F1PF2=
，则
=
。
三、解答题（共74分）试题见答题卷。
高三数学模拟试卷（一）答卷
一、选择题答案（本大题共12小题，每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
|
二 、填空题（本大题共4小题，每小题4分，共16分，把答案填在题后的
横线上）
１３。 。
１４。 。
１５。 。
１６。 。
三、解答题（本大题共6小题，共74分。解答应写出文字说明，证明过程和演算步骤）
17．（本题满分12分）向量
与
满足
，且夹角为60°，
，（
。
（1） 求函数
的解析式。
（2） 当
且
时，求向量
与向量
的夹角。
18．（本题满分12分）
在棱长为2的正方体ABCD—A1B1C1D1中，M、N分别是A1B1和B1B的中点。
（1） 求直线AM和CN所成角的大小；
（2） 若P为B1C1的中点，求证：B1D⊥平面PMN；
（3） 
求点A到平面PMN的距离。
19．（本题满分12分）
数列
的前n项和为Sn，且
。
（1） 若等差数列
恰好使数列
成公比为
的等比数列，
求通项
（2） 求通项
（3） 求
的值
20．（本题满分12分）有三种产品，合格率分别是0.90，0.95和0.95，各抽取一件进行检验。
（１） 求恰有一件不合格的概率；（精确到0.001）
（２） 求至少有两件不合格的概率。（精确到0.001）
21．（本题满分12分）如图，已知点F（0，1），直线L：y=-2，及圆C：
。
（1） 若动点M到点F的距离比它到直线L的距离小1，求动点M的轨迹E的方程；
（2） 过点F的直线g交轨迹E于G（x1，y1）、H（x2，y2）两点，求证：x1x2 为定值；
（3） 
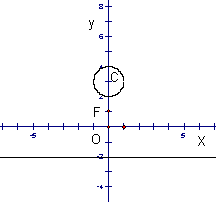过轨迹E上一点P作圆C的切线，切点为A、B，要使四边形PACB的面积S最小，求点P的坐标及S的最小值。
22．（本题满分14分） 已知函数对任意实数x都有
，且当
时，
。
（1） 当
时，求的表达式。
（2） 证明是偶函数。
（3） 试问方程
是否有实数根？若有实数根，指出实数根的个数；若没有实数根，请说明理由。
答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | B | D | C | C | D | A | D | B | C | C | C |
填空题 13、-5 14、
15、
16、-
解答题
17、①f(x)=2x2+15x+7 ②θ=Л-arccos
18 ①夹角arccos
②略 ⑶ 19 ①bn=-3n+2 ②an=()n-1+3n-2
⑶ 20 ①0.176 ② 0.012 21 ①x2=4y ②x1x2=-4 ⑶P(±2,1) SMIN=
22 ①f(x)=
(2k≦x≦2k+2,
k∈Z) ②略 ⑶方程在[1，4]上有4个实根