高三数学第一学期期末抽测试卷
一、填空题 (每小题4分，共48分)
1. 已知复数
满足：
，则
__________.
2. 函数
的最小正周期为____________.
3. 设
是三个集合，则“
”是“
”的___________________条件.
4. 已知函数
，则
________.
5. 设
，若
，则
________.
6. (理) 
两点的极坐标分别为
，则两点的距离
_______.
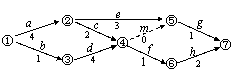
(文) 某工程的工序流程图如图，
则该工程的总工时为________(天).
7. 某品牌42英寸等离子彩电经过4次降价，价格由原来的6.5万元降至当前的4万元，若每次
降幅相同，则每次降低的百分率为__________(精确到0.1%).
8. 
__________.
9. 学校新年联欢会原定的5个节目已排成节目单，开演前又增加了两个新节目. 如果将这两个
节目插入原节目单中，那么不同插法的种数为_________(用数值表示).
10. 已知函数
是定义在
上的奇函数，且
，当
时，
，
则
___________.
11. 观察下列式子：
，则可以猜想的结论
为：___________________________.
12. 记
，函数
，则使函数
为偶函数
的最小的自然数
的值等于__________.
二、选择题 (每小题4分，共16分)
13. 若
为复数，下列结论正确的是
( )
A. 若
B. 
C. 若
则为纯虚数
D. 若
是正实数，那么一定是非零实数
14. 若
则
的最小值是 ( )
A. 
B. 
C. 
D. 
15.(理) 圆锥曲线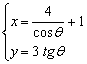
(
为参数) 的焦点坐标为 ( )
A. 
B. 
C. 
D. 
(文)已知
满足不等式组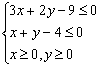
，则使
取得最大值的点的坐标为 ( )
A. 
B. 
C.
D.
16. 已知集合
，
, (
可以等于
)，从集合
中任取一元素，则该元素的模为
的概率为 ( )
A. 
B. 
C. 
D. 
三、解答题 (本大题共86分)
17. (满分12分)
已知
、是实系数一元二次方程的两个根，若、满足方程
，
求、.
18. (满分12分) 已知
(1) 当
时，求不等式的解；
(2) 若
的取值范围构成的集合为空集，求实数
的取值范围.
19. (满分14分) 已知定义在区间
上的函数
的图象关于直线
对称，
当
时，函数
，其图象如图所示.
(1) 求函数在的表达式；
(2) 求方程
的解.
20. (满分14分)
2003年10月15日，我国的“长征”二号
型火箭成功发射了“神州”五号载人飞船，这标志着中国人民又迈出了具有历史意义的一步.火箭的起飞重量
是箭体(包括搭载的飞行器)的重量
和燃料重量之和. 在不考虑空气阻力的条件下，当装载燃料重量不同时，火箭的最大速度
满足函数关系式: 
(其中
)，当燃料重量为
(吨) (
为自然对数的底数)时，该火箭的最大速度为4 (千米/秒).
(1)求长征二号系列火箭的最大速度（千米/秒）与燃料重量(吨)之间的函数关系式;
(2)已知“长征”二号型火箭的起飞重量是479.8吨，则应装载多少吨燃料 (精确到0.1吨)
才能使该火箭的最大飞行速度达到7.9千米/秒, 顺利地把飞船发送到预定的椭圆轨道？
21. (满分16分) 已知数列
满足：
，
，数列
的前项和
.
(1) 求数列和
的通项公式；
(2) 设
.
(理) 是否存在
，使
成立？并说明理由.
(文) 求使
的自然数的值.
22. (满分18分) 函数
的定义域为
（为实数）.
(1)
当
时，求函数
的值域；
(理) (2) 若函数在定义域上是减函数，求的取值范围；
(3)
函数在
上的最大值及最小值，并求出函数取最值时的值.
(文) (2) 若
时，判断函数
的单调性并证明；
(3)
若
在定义域上恒成立，求的取值范围.
高三数学第一学期期末抽测试卷 参考答案
一、填空题 1. 
2. 
3. 必要非充分条件 4. 
5. 11 6. (理)
(文) 9
7.
11.4% 8. 2 9. 42 10. 
11. 
12. 3
二、选择题 13. D 14. C 15. (理) C (文) B 16. D
三、解答题
17．当
、是实数时，
，
或
，当、是虚数时，设
，则
，代入方程得
，
，
，
.
18. （1）由
得
，由
得
，∵
，∴
。
（2）由已知，
或
，即
或
。
19．（1）当
时，函数
，观察图象易得：
，即时，函数
，由函数
的图象关于直线
对称得，
时，函数
. ∴
.
（2）当时，由
得，
；当时，
由
得，
.∴方程
的解集为
20．（1）以
,
，代入函数式可得
，则
(或
);
（2）设装载
吨燃料方能满足题意，此时
，即
解得
21．（1）由
，∴
，
。
由
及
，可得
，
令
，则
也满足上式，∴
.
（2）(理)
，设
为数列
中的最大项，则
，∴
。
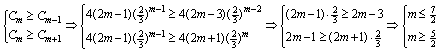即
为中的最大项。∵
，∴不存在
，使
成立。
(文)∵,∴
.
设
，
，
，
，
，
，
。当
时，
,即
。故
在
上单调递减。
∴使
的自然数
的值为2，3，4，5.
22．（1）显然函数
的值域为
；
(理)（2）若函数在定义域上是减函数，则任取
且
都有
成立，
即
只要
即可，由，故
，所以
，
故
的取值范围是
；
（3）当
时，函数在上单调增，无最小值，当
时取得最大值
；
由（2）得当时，函数在上单调减，无最大值，当时取得最小值；
当
时，函数在
上单调减，在
上单调增，无最大值，
当
时取得最小值
.
(文)（2）当
时在上为单调增函数。证明如下：任取且，
则
，所以在上为单调增函数。
（3）当
时
在定义域上恒成立，即
在时恒成立。
设
，当时
，只要
即可，的取值范围是
。
也可利用求在上的最小值的方法来解：时无最小值
；
。